Назва роботи: Побудова графіків в Mathcad
Предметна область: Інформатика, кібернетика та програмування
Опис: Для цього нам необхідно знати рівняння графіків дотичній і нормалі. Їх я не знав, тому довелося звернутися до всемогутнього інтернету. У ньому я знайшов сайт, нехай береже його могутній браузер Mozilla Firefox, який показав мені, дурному холопу, рівняння потрібних мені функцій.
Розмір файлу: 181.5 KB
Роботу скачали: 38 чол.
Міністерство Освіти і науки РФ
РИБИНСЬКИЙ ДЕРЖАВНИЙ АВІАЦІЙНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ імені. П.А.СОЛОВЬЕВА
Факультет Радіотехніки, електроніки та інформатики
інформатика
Студент групи СПД-13 Пестов В.В.
Код Підпис, дата П.І.Б
Викладач Пинаев В.Н.
Для заданої функції.
1. Побудувати графік функції і графіки її першої та другої похідної в загальних координатах.
2. Побудувати графіки дотичній і нормалі до функції в точці (x 0 = 3) 0.
3. Знайти точки локального екстремуму функції f (x) і точки перегину (стаціонарні точки).
4. Визначити значення функції в стаціонарних точках.
5. Визначити первісну + c і побудувати графіки сімейства первісних.
1. Побудувати графік функції і графіки її першої та другої похідної в загальних координатах.
Для побудови графіка функції і двох її похідних в Mathcad нам необхідно отримати рівняння похідних першого та другого ступенях. Це можна зробити і самому, не використовуючи ніяких програм:
f '(x) = x' * e - x + x * (e - x) '= e - x - x * e - x = e - x * (1 x)
Тепер, коли я обчислювальні обидві похідні, саме час побудувати їх графіки в Mathcad. Що у мене вийшло, можна побачити на рис.1:
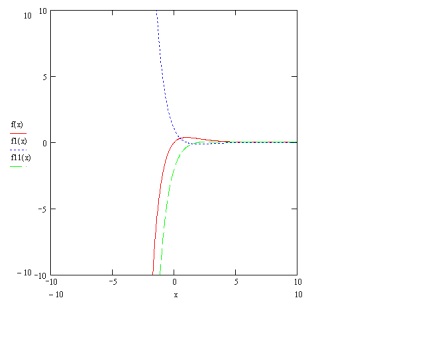
Червоною лінією зображено графік самої функції, зеленої і синьої - графіки першої і другої її похідних відповідно.
Отже, перше завдання виконано.
2. Необхідно побудувати графіки дотичній і нормалі до графіка функції.
Рівняння дотичної виглядає так:
y = f '(x 0) * x + f (x 0) -f' (x 0) * x 0
Рівняння нормалі має вигляд:
y = f (x 0) - (x-x 0) / f '(x 0)
Де х 0 = 3 (точка, задана за умовою).
Тепер, коли у мене з'явилися рівняння, залишилося записати їх в програмі Mathcad. Ось які графіки у мене вийшли (рис.2):
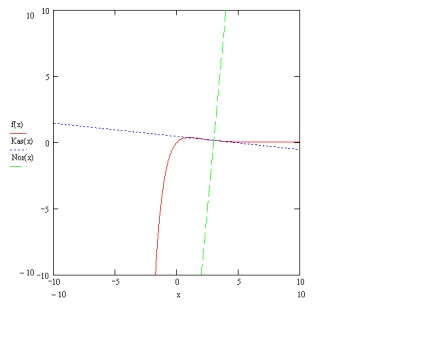
Червона лінія - графік функції, синій - дотична до графіка в точці х 0. зелений - нормаль до графіка в точці х 0.
Завдання 2 можна вважати виконаним.
3. Знайти точки локального екстремуму функції f (x) і точки перегину (стаціонарні точки).
Щоб знайти точки локального екстремуму, необхідно прирівняти першу похідну функції до нуля.
f '(x) = 0; e - x * (1 x) = 0; 1 x = 0;
x = 1 - критична точка, вона ж буде і стаціонарної (критична точка - точка, де функція змінює своє "напрям": якщо вона зростала, то починає спадати (в моєму випадку) і навпаки). Стаціонарна точка - точка, в якій похідна дорівнює нулю.
З цим завданням я теж впорався.
4. Визначити значення функції в стаціонарних точках.
Ну це зовсім просто. Досить підставити точку х = 1 в рівняння функції:
Я вирішив представити значення і в чисельному вигляді, воно буде дорівнює:
Ось і це завдання виконано, залишилося останнє.
5. Визначити первісну + c і побудувати графіки сімейства первісних.
Я дозволив собі не міняти мову, так як я не хотів порушувати всю чарівну форму даного сайту. І ось у мене тепер є рівняння первісної. Але мені то треба побудувати сімейство первісних. Я вже почав хвилюватися, адже у мене всього одна формула, а мені треба побудувати кілька графіків, поки мені не підказали, що потрібно всього-то міняти Constant. І ось я вже в Mathcad пишу формули і, о диво, у мене готові графіки сімейства первісних (рис.3):
Червоною лінією позначений графік первісної, де const = 0, а для інших const = 4; -4 відповідно.
Ось і виконана моя курсова робота. Пора підвести підсумки.
В ході виконання цієї роботи, я пізнав таку чудову програму, як Mathcad. придбав невеликі навички в поводженні з нею, а також в черговий раз переконався в такому непорушно величному творінні людини, як інтернет, бо перед ним ми повинні падати на коліна, адже це наше дітище, яке майже зневолило нас. І я, мерзенний холоп, прихиляється перед ним. А також я дякую своїх наставників, Пинаева Володимира Миколайовича та Шалаєва Дмитра Сергійовича, завдяки яким, такий холоп, як я, дізнався і зміг освоїти програму Mathcad.