У діелектриках швидкість світлових ЕМВ залежить від частоти. Це явище називається дисперсією. Вплив дисперсії проявляється лише в поширенні немонохроматичним хвиль, тому що її монохроматические складові з різними частотами поширюються з різними швидкостями. Дисперсія є наслідком залежності поляризованности атомів від частоти. Для знаходження явного вигляду e (w), що входить в матеріальні рівняння, скористаємося мікроскопічної класичною теорією взаємодії електромагнітного поля хвилі з речовиною. Мікроскопічна теорія виходить з деякої ідеалізованої моделі будови речовини. Найбільшою простотою відрізняється модель газоподібного середовища, тому що для неї в першому наближенні можна не враховувати взаємодію атомів або молекул і вважати, що чинне на окремий атом поле збігається із середнім полем ЕМВ. В таких умовах для отримання макроскопічного матеріального рівняння досить розглянути дію поля ЕМВ на ізольований атом. Взагалі кажучи, застосовувати класичну теорію до таких процесів потрібно вкрай обережно. Але в даному випадку квантова теорія дисперсії призводить до таких же результатів, що і класична.
У класичній теорії дисперсії електрон, з яким взаємодіє електромагнітне поле (зовнішній, або оптичний електрон), в атомі розглядається як згасаючий дипольний осцилятор, що характеризується певною власною частотою Wо і постійної загасання g, так що рівняння його руху в поле E (t) = Eo e - iwt світлової хвилі має вигляд:
де r - зміщення електрона з положення рівноваги. Будемо шукати рішення цього рівняння у вигляді:
В результаті отримаємо:
Дипольний момент атома p (t), індукований полем E (t):
Якщо N - концентрація електронів з власною частотою коливань w0. то полярізованностьP середовища визначається наступним чином:
З іншого боку поляризованность середовища (полярізаціясреди) дорівнює
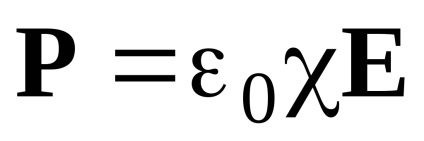
де c - лінейнаядіелектріческаявоспріімчівостьсреди. яка взагалі кажучи, залежить від частоти w. Врахуємо також, що вектори D. E і P пов'язані співвідношенням:
Тоді з (4.10) і (4.11) випливає, що для відносної проникності :, (4.12)
а з (4.8), (4.9), (4.10) маємо:
Оскільки
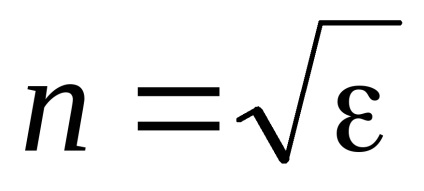
Тоді з урахуванням (4.14) маємо рівняння:
Для прозорих або частково прозорих в оптичному діапазоні діелектриків g дуже мало. тоді
З цього наближення отримуємо:
Якщо в середовищі дисперсію визначають різні ансамблі електронів з власними частотами w0i і концентрацією Ni. то формулу (4.18) можна узагальнити:
У цій формулі не враховано коливання іонів. Оскільки їх маса значно більше маси електронів, то власні частоти іонів лежать в далекій інфрачервоній області.
9Нормальная дисперсія. Далеко від власних резонансів величина
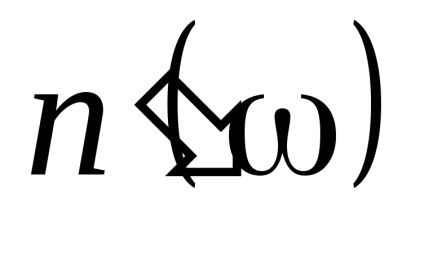
Г
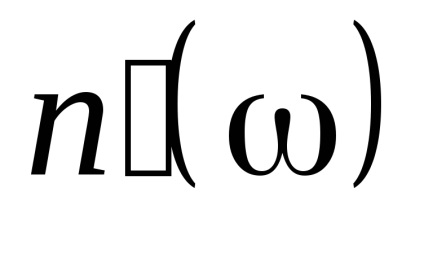
Якщо дійсна частина показника заломлення збільшується зі зростанням частоти, то дисперсія називається нормальною. Нормальна дисперсія спостерігається у всій області прозорості діелектріков.Для малих частот (w <
Це значення може істотно відрізнятися від значення показника заломлення для оптичних частот. (Наприклад, для води в області оптичних частот n = 1,33. А статичне значення
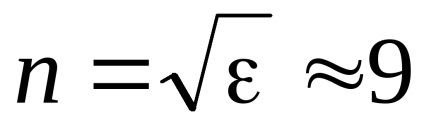
Для великих частот (w >> w0i), при цьому
Т.ч. для короткохвильового випромінювання діелектрик є оптично менш щільною середовищем, ніж вакуум. Наприклад, для рентгенівського випромінювання може спостерігатися повне відображення. Крім того, при дуже високих частотах характер зв'язку електронів ролі не грає, а показник заломлення n залежить лише від загальної концентрації всіх електронів.
Аномальна дисперсія. Нехтування загасанням (g = 0) призвело до того, що
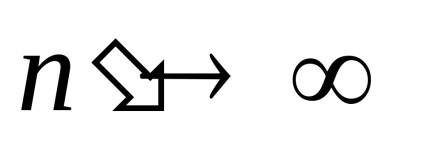
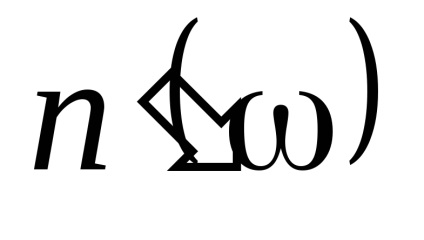
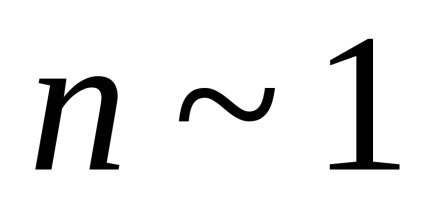
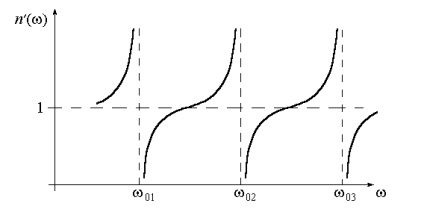
Дисперсійні криві (4.24) представлені на рис.4.2.
Поблизу резонансної частоти w0 показник заломлення
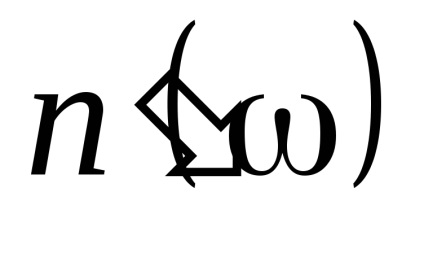
явище називається аномальнойдісперсіей.