Продовжуємо підготовку до ЄДІ з інформатики та сьогодні розглянемо рішення задач типу A10.
Завдання цього типу досить складні. Підходити до їх вирішення, не знаючи основ логіки не варто. Тому настійно рекомендую прочитати про кон'юнкцію. диз'юнкцію. імплікації.
На числовій прямій дано два відрізки: P = [1, 39] і Q = [23, 58].
Виберіть із запропонованих відрізків такий відрізок A, що логічне вираз
((X ∈ P) → ¬ (x ∈ Q)) → ¬ (x ∈ А)
тотожно істинна, тобто приймає значення 1 при будь-якому значенні змінної х.
1) [5, 20] 2) [25, 35] 3) [40, 55] 4) [20, 40]
Для зручності давайте позначимо наші прості висловлювання великими латинськими літерами (за назвою відрізків):
Перепишемо наше вираз в більш зручному вигляді:
Завдання 10 ЄДІ з інформатики
Тепер невеликий відступ про імплікації. Імплікації можна виразити через диз'юнкцію і заперечення ось таким чином:
Розкриття імплікації через диз'юнкцію і заперечення
Це дуже важливе правило і його необхідно запам'ятати.
Тепер ми можемо переписати наше висловлювання, пішовши від імплікації:
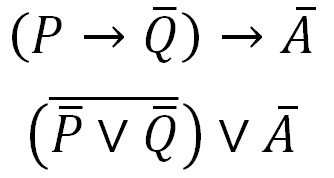
Щоб спростити вираз в дужках скористаємося законом де Моргана (другий на картинці)
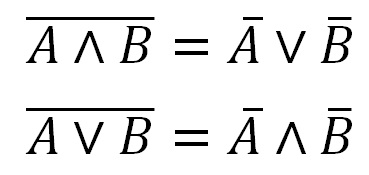
Закони де Моргана
В результаті отримаємо
Застосувавши закон подвійного заперечення отримаємо підсумкове висловлювання з якому і будемо працювати далі. Так, це ще не все
Тепер давайте згадаємо, що наші висловлювання - це відрізки і відобразимо їх на координатній прямій.
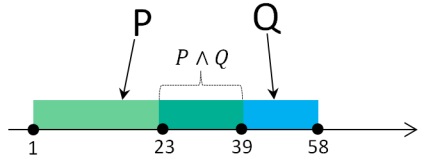
Графік для завдання
Проаналізуємо графік і підсумкове висловлювання. Підсумкове висловлювання повинно бути істинним при будь-якому значенні х за умовою задачі. У підсумковому висловлюванні у нас вираз в дужках і інверсія A з'єднані диз'юнкція. Диз'юнкція істинна коли хоча б одне або обидва висловлювання істинними. Значить підсумкове висловлювання буде істинним коли або вираз в дужках істинно, або заперечення A істинно, або істинні обидва вирази (в дужках і заперечення A). Вираз в дужках - кон'юнкція, а вона істинна тільки коли обидва висловлювання істинними. Т. е. Коли x належить проміжку [23, 39] підсумкове висловлювання буде істинним. В іншому випадку висловлювання буде хибним і тоді заперечення A має бути істинним. Раcсмотрім, коли воно таким буде.
На початку ми визначилися, що висловлювання A означає, що x ∈ А. Так як воно у нас з запереченням, то заперечення A означатиме, що x ∉ A, а значить точка x повинна належати діапазону [-∞, 23] або [39 , + ∞]. Залишилося знайти такий відрізок A, який буде перекривати діапазон [23, 39] (так як у нас він з запереченням, то в підсумку вийде потрібний нам діапазон). Т. е. Ліва координата відрізка повинна бути більше або дорівнює 23, а права менше або дорівнює 39.
Із запропонованих варіантів підходить тільки [25, 35]. Правильна відповідь - 2.
Ще один приклад вирішення завдання A10 ЄДІ з інформатики (на прохання Євгенії).
На числовій прямій дано три відрізка:
P = [0,40], Q = [20,45] і R = [10,50].
Виберіть такий відрізок A, що формула ((x∈P) → (x∈Q)) ∨ ((x∉A) → (x∉R)) тотожно істинна, тобто приймає значення 1 при будь-якому значенні змінної х.
1) [5,20] 2) [10,15] 3) [15,20] 4) [35,50]
Для зручності приймемо такі позначення:
Тепер нашу формулу ми зможемо переписати в такому вигляді:
Застосувавши закон де Моргана, отримаємо наступне:
Для зручності позначимо вираження в дужках так:
Залишилося відобразити формулу на числовій прямій.
Розглянемо вираз Z і перенесемо його на числову пряму
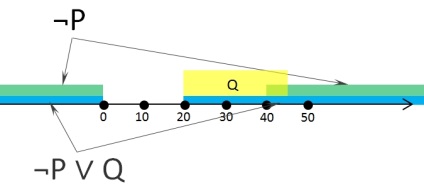
Тут у нас зеленим кольором позначена область ¬P, жовтим - Q, а блакитним - область ¬P ∨ Q.
Тепер зауважимо, що вирази в дужках об'єднані диз'юнкція. а це значить, що підсумкове вираз буде тотожно істинним коли хоча б одне або обидва відразу вираження в дужках істинні.
Зараз ми бачимо, що якщо змінна х належить діапазону [-∞; 0] або [40; + ∞], то підсумкове вираз було це слово.
Розглянемо другий вираз A ∨ ¬R (я видалив на попередньому малюнку області ¬P і Q, щоб вони не заважали, залишивши тільки кінцеву область ¬P ∨ Q):
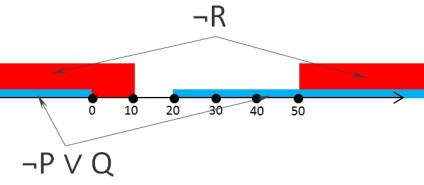
Рішення завдання A10 ЄДІ з інформатики
Як бачимо, вираз у другій скобці було це слово тільки коли x належить діапазону [-∞; 10] або [50; + ∞]. Загальна вираз буде істинно коли x належить діапазону [-∞; 10] або [20; + ∞].
А ось якщо x знаходиться в діапазоні (10; 20), то підсумкове вираз буде хибним. Значить нам треба знайти таке значення діапазону A, яке перекриє діапазон (10; 20). Із запропонованих в умови варіантів цій умові задовольняє тільки діапазон [5,20].