Що таке алгебра логіки?
Алгебра логіки (булева алгебра) - це розділ математики, який виник в XIX столітті завдяки зусиллям англійського математика Дж. Буля. Спочатку булева алгебра не мала ніякого практичного значення. Однак уже в XX столітті її положення знайшли застосування в описі функціонування і розробці різних електронних схем. Закони та апарат алгебри логіки став використовуватися при проектуванні різних частин комп'ютерів (пам'ять, процесор). Хоча це не єдина сфера застосування даної науки.
Що ж собою являє алгебра логіки? По-перше, вона вивчає методи встановлення істинності чи хибності складних логічних висловлювань за допомогою алгебраїчних методів. По-друге, булева алгебра робить це таким чином, що складне логічне висловлювання описується функцією, результатом обчислення якої може бути або істина, або брехня (1, або 0). При цьому аргументи функції (прості висловлювання) також можуть мати тільки два значення: 0, або 1.
Що таке просте логічне висловлювання. Це фрази типу «два більше одного», «5.8 є цілим числом». У першому випадку ми маємо істину, а в другому брехня. Алгебра логіки не стосується суті цих висловлювань. Якщо хтось вирішить, що висловлювання «Земля квадратна» істинно, то алгебра логіки це прийме як факт. Справа в тому, що булева алгебра займається обчисленнями результату складних логічних висловлювань на основі заздалегідь відомих значень простих висловлювань.
Логічні операції. Диз'юнкція, кон'юнкція і заперечення
Так як же зв'язуються між собою прості логічні висловлювання, утворюючи складні? У природній мові ми використовуємо різні союзи і інші частини мови. Наприклад, «і», «або», «або», «не», «якщо», «то», «тоді». Приклад складних висловлювань: «у нього є знання і навички», «вона приїде у вівторок, або в середу», «я буду грати тоді. коли зроблю уроки »,« 5 не дорівнює 6 ». Як ми вирішуємо, що нам сказали правду чи ні? Якось логічно, навіть десь несвідомо, виходячи з попереднього життєвого досвіду, ми розуміє, що правда при союзі «і» настає в разі правдивості обох простих висловлювань. Варто одному стати брехнею і все складне висловлювання буде брехливо. А ось, при зв'язці «або» має бути правдою тільки одне просте висловлювання, і тоді все вираз стане справжнім.
Булева алгебра переклала цей життєвий досвід на апарат математики, формалізувала його, ввела жорсткі правила отримання однозначного результату. Союзи стали називатися тут логічними операторами.
Алгебра логіки передбачає безліч логічних операцій. Однак три з них заслуговують на особливу увагу, тому що з їх допомогою можна описати всі інші, і, отже, використовувати менше різноманітних пристроїв при конструюванні схем. Такими операціями є кон'юнкція (І), диз'юнкція (АБО) і заперечення (НЕ). Часто кон'юнкцію позначають . диз'юнкцію - ||. а заперечення - рисою над змінної, що позначає висловлювання.
При кон'юнкції істина складного вираження виникає лише в разі істинності всіх простих виразів, з яких складається складне. У всіх інших випадках складне вираз буде неправдою.
При диз'юнкції істина складного вираження настає при істинності хоча б одного вхідного в нього простого вираження або двох відразу. Буває, що складне вираз складається більш, ніж з двох простих. В цьому випадку достатньо, щоб одне просте було істинним і тоді все висловлювання буде істинним.
Заперечення - це унарна операція, т.к виконується по відношенню до одного простого висловом або по відношенню до результату складного. В результаті заперечення виходить нове висловлювання, протилежне вихідного.
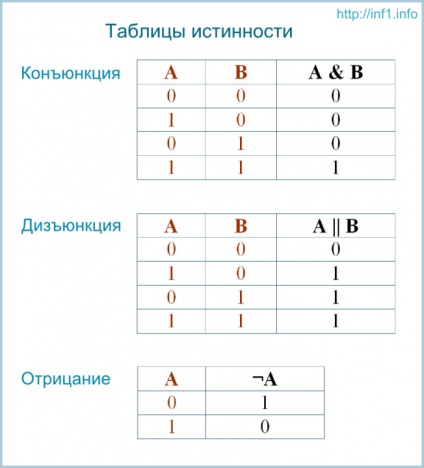
таблиці істинності
Логічні операції зручно описувати так званими таблицями істинності. в яких відображають результати обчислень складних висловлювань при різних значеннях вихідних простих висловлювань. Прості висловлювання позначаються змінними (наприклад, A і B).
Логічні основи комп'ютера
У ЕОМ використовуються різні пристрої, роботу яких прекрасно описує алгебра логіки. До таких пристроїв відносяться групи перемикачів, тригери, суматори.
Крім того, зв'язок між булевої алгеброю і комп'ютерами лежить і в використовуваної в ЕОМ системі числення. Як відомо вона двоичная. Тому в пристроях комп'ютера можна зберігати і перетворювати як числа, так і значення логічних змінних.
переключательние схеми
У ЕОМ застосовуються електричні схеми, що складаються з безлічі перемикачів. Перемикач може перебувати тільки в двох станах: замкнутому і розімкнутому. У першому випадку - струм проходить, у другому - немає. Описувати роботу таких схем дуже зручно за допомогою алгебри логіки. Залежно від положення перемикачів можна отримати або не одержати сигнали на виходах.
Вентилі, тригери і суматори
Вентиль являє собою логічний елемент, який приймає одні двійкові значення і видає інші в залежності від своєї реалізації. Так, наприклад, є вентилі, реалізують логічне множення (кон'юнкцію), додавання (диз'юнкцію) і заперечення.
Тригери і суматори - це відносно складні пристрої, що складаються з більш простих елементів - вентилів.
Тригер здатний зберігати один двійковий розряд, за рахунок того, що може перебувати в двох стійких станах. В основному тригери використовується в регістрах процесора.
Суматори широко використовуються в арифметико-логічних пристроях (АЛП) процесора і виконують підсумовування двійкових розрядів.
Зображення, використані в статті