Кожна i-я вершина дерева зв'язується з розширеною розміткою m (i). У розширеній розмітці число міток в позиції може бути або невід'ємним цілим, або нескінченно великою. Нескінченне число міток позначимо символом w. ()
Вершини класифікуються на 4 види:
Граничними є вершини, кото-які ще не оброблені алгоритмом.
Алгоритм починає свою роботу з завдання початковоїрозмітки. До тих пір, поки є граничні вершини, вони обробляються алгоритмом.
Нехай x - гранична вершина, яку необхідно обробити, і з якою пов'язана розмітка m (x).
1. Якщо для розмітки m (x) на один з переходів неразрешeн, тобто m (x) тупикова розмітка, то x термінальна вершина.
2. Якщо в дереві є інша вершина y. яка не є граничною, і з нею пов'язана розмітка m (y) = m (x), то вершина x дублююча.
3. Для будь-якого переходу tj, з безлічі T, дозволених в розмітці m (x), створити нову вершину z дерева досяжності. Розмітка m (z), пов'язана з цією вершиною, визначається для кожної позиції рi наступним чином:
ii. якщо на шляху з кореня дерева в z є вершина y така, що tj і
то m (z) i = w;
iii. у іншим способом
Дуга, позначена tj, спрямована від вершини х до вершини z. Вершина x переопределяется як внутрішня, вершина z стає граничної.
Коли всі вершини дерева стають термінальними, дублюючими або внутрішніми, алгоритм зупиняється.
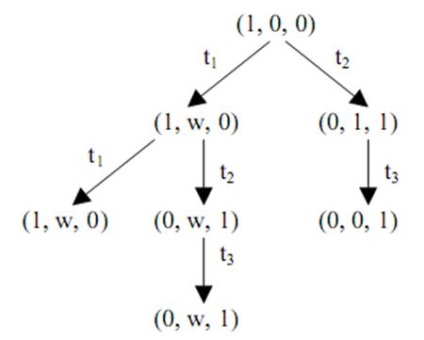
Кінцеве дерево досяжності
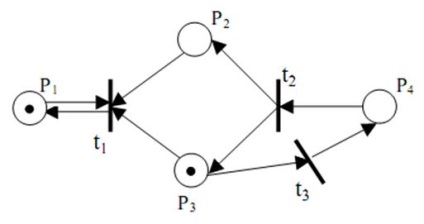
Перехід tj мережі Петрі С називається потенційно запустімим в маркуванні # 956 ;, якщо в R (C, # 956;) існує маркування # 956; ', в якій tj дозволений.
Перехід активний в маркуванні # 956 ;, якщо потенційно запустимо у всякій маркування з R (C, # 956;).
o Рівень 0: Перехід tj ніколи не може бути запущений.
o Рівень 1. Перехід tj потенційно запустимо.
o Рівень 2: Для будь-якого цілого n існує послідовність запусків, в якій перехід tj присутній принаймні n раз
o Рівень 3. Існує нескінченна послідовність запусків, в якій перехід tj присутній необмежену кількість разів.
o Рівень 4. для будь-якої # 956; ' з R (C, # 956;) існує така послідовність запусків # 963 ;, що перехід tj дозволений в # 948; (# 956; `, # 963;).
Перехід, що володіє активністю рівня 0, називається пасивним.
Перехід, що володіє активністю рівня 4, називається активним.
Мережа Петрі володіє активністю рівня i, якщо кожен її перехід володіє активністю рівня i.
Мережа Петрі з переходами різних рівнів
t1 - перший рівень
t2 - другий рівень
t3 - третій рівень
Деякі види мереж Петрі:
Тимчасова мережа Петрі - переходи мають вагою, визначальним тривалість спрацьовування (затримку).
Стохастична мережа Петрі - затримки є випадковими величинами.
Функціональна мережу Петрі - затримки визначаються як функції деяких аргументів, наприклад, кількості міток в будь-яких позиціях, стану деяких переходів.
Кольорова мережу Петрі - мітки можуть бути різних типів, які охоплюють квітами, тип мітки може бути використаний як аргумент в функціональних мережах.
Інгібіторна мережі Петрі - можливі інгібіторні дуги, що забороняють спрацьовування переходу, якщо у вхідній позиції, пов'язаної з переходом ингибиторной дугою знаходиться мітка.
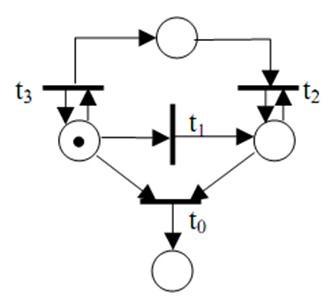
Процеси виникнення і усунення несправностей в деякій технічній системі, що складається з безлічі однотипних блоків. У резерві є один справний блок; відомі статистичні дані про інтенсивності виникнення відмов і длительностях таких операцій, як пошук несправностей, заміна і ремонт відмовив блоку. Пошук і заміну відмовив блоку виробляє одна бригада, а ремонт заміненого блоку - інша бригада
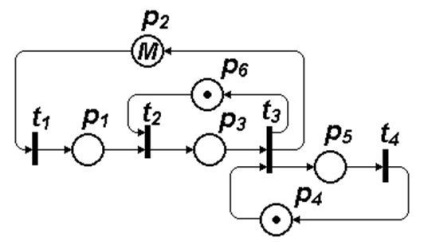
M відповідає числу наявних в системі блоків.
t1 - відмова блоку - проміжок часу між відмовами
t2 - пошук несправного блоку, - тривалість пошуку
t3 заміна несправного блоку - тривалість заміни
t4 - закінчення ремонту - тривалість ремонту.
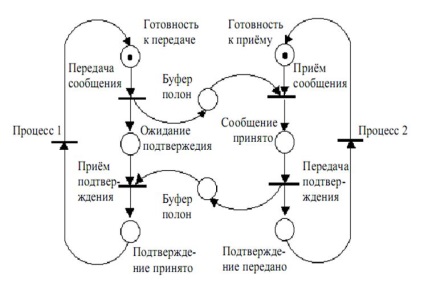
Спрощена модель протоколу обміну даними між двома процесами