20'Прінціпи обліку слабкою заповнювання мережевих матриць при використанні методу Гаусса.
1) Порядок виключення ненульових елементів в методі Гаусса повинен бути таким, щоб в процесі виключення з'явилися мінімальна к-ть нових ненульових елементів;
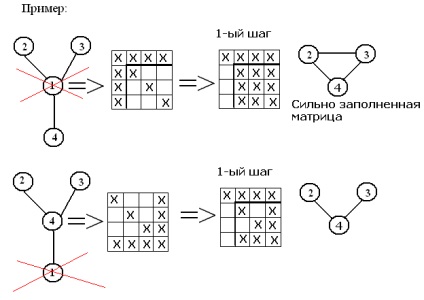
Підсумок: 1) Треба щось змінювати порядок проходження вихідних вузлів
2) Або не зраджуючи порядку винятку перейменовуючи вузли (див квиток 23)
Порядок виключення: в першу чергу повинні виключатися вузли найменше пов'язані з іншими вузлами (що мають найменшу кількість інцидентних зв'язків з іншими елементами)
2) Зберігати в пам'яті машини потрібно тільки ненульові елементи і тільки з ними потрібно проводити арифметичні операції (див квиток 24)
21'Порядок виключення невідомих в методі Гаусса з зворотним ходом.
1) Порядок виключення ненульових елементів в методі Гаусса повинен бути таким, щоб в процесі виключення з'явилися мінімальна к-ть нових ненульових елементів;
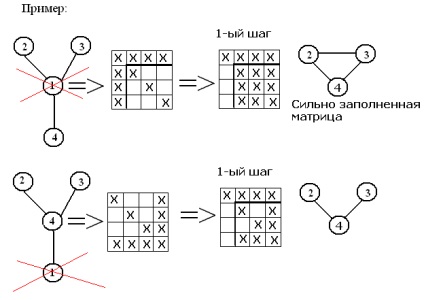
Підсумок: 1) Треба щось змінювати порядок проходження вихідних вузлів
2) Або не зраджуючи порядку винятку перейменовуючи вузли (див квиток 23)
Порядок виключення: в першу чергу повинні виключатися вузли найменше пов'язані з іншими вузлами (що мають найменшу кількість інцидентних зв'язків з іншими елементами)
2) Зберігати в пам'яті машини потрібно тільки ненульові елементи і тільки з ними потрібно проводити арифметичні операції (див квиток 24)
22 'Коефіцієнт заповнюваності матриць. Зберігання ненульових елементів матриць.
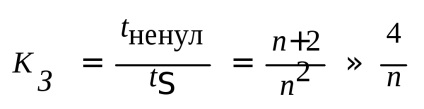
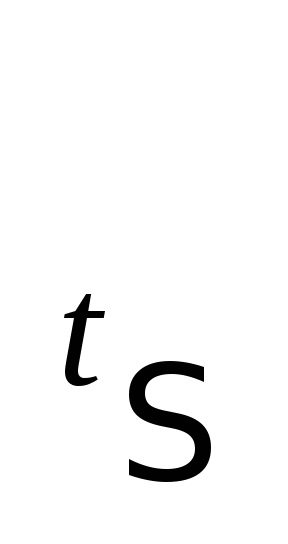
У великих схемах
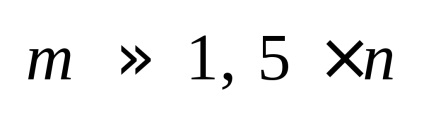
Висновок: чим більше кількість вузлів схеми тим менше коефіцієнт заповненості
Зберігати необхідно тільки ненульові елементи матриці Y, причому тільки верхній Δ, так як матриця Y - симетрична
Вимоги до схем зберігання матриць.
2) Простота формування
3) Простота використання
а) простота вибірки елементів
б) гнучкість зміни інформації, що зберігається
(Тому що поле 1 кроку поява. Нові ненул елементи)
I. Задаємо тільки ненул. елементи:
23 'Алгоритми впорядкування, їх класифікація.
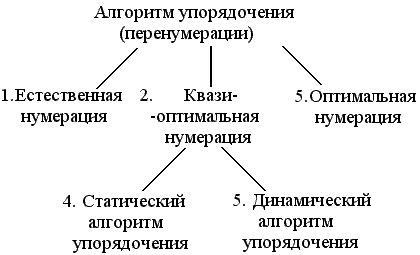
2) компроміс між програмно не надто складною Перенумерація і економією пам'яті машини
3) процес упорядкування проходить до початку виключення вузлів
4) здійснюється на кожному кроці прямого ходу
5) нумерація, що припускає мінім. необхідний обсяг пам'яті, хв. сумарне кількість ненульових елементів
При програмної перенумерации відбувається тільки імітація процесу виключення невідомих
24 'Зберігання слабозаполненних матриць. Схеми упаковки матриць. Вимоги до схем зберігання матриць.
2) Простота формування
3) Простота використання
а) простота вибірки елементів
б) гнучкість зміни інформації, що зберігається
(Тому що поле 1 кроку поява. Нові ненул елементи)
I. Задаємо тільки ненул. елементи:
Створюється доп масив NADR - номер комірки масиву VALUE, з якого починаються провідності, пов'язані з цим вузлом
7 - тому що 6 ел-тів за все в VALUE, показує що більше ні з чим не пов'язано.
26 'Алгоритмічна і програмна реалізація формування матріциYв компактній формі .См.25 Програма:
Subroutine ysz (nn, nk, z, yc, y, diag, nzero, value, icol, nadr, n, m)
Complex z (m), yc (m), diag (n), value (1)
Dimension nzero (n), icol (1), nadr (n)
if (i1 * i2.ne.0) then j = i2
nadr (i) = nadr (i-1) + nzero (i-1)
if (i1 * i2.ne.0) then j = i2
end do end return
27 'Ітераційні методи розрахунку УР. Алгоритм розрахунку УР методом Зейделя.
1) повузлова методи - м. Де вих змінні шукаються з кожного слід. ур-я послідовно.
2) Одноврем. реш. ур. - все ур. системи реш-ся одночасно на кожній ітерації.
Бал.токов: метод Гаусса, звернення, факторизации матриці
Бал. Потужностей: метод Ньютона
1) кількість обчислень на кожн. ітерації;
2) сумарна кількість ітерацій;
3) сумарний час обчислень.
Немає абсолютно ефективних і абсолютно сходяться методів
28 'Метод Зейделя стосовно вирішення нелінійного вузлового ур-я в формі балансу струмів.