Якщо дуга гасне при першому проходженні високочастотного струму через нуль (момент t2), то на ємностях здорових фаз залишаються заряди СUBмакс і СUCмакс (для рис.1.2 UВмакс = UВмакс), а на ємності С фази А заряд дорівнює нулю.
Після гасіння дуги сумарний заряд розподілиться порівну між ємностями 3-х фаз, які придбають однакову додаткову напругу по відношенню до землі U (зміщення нейтралі), накладається на напругу джерела.
Для розглянутого випадку, оскільки UВмакс = UCмакс.
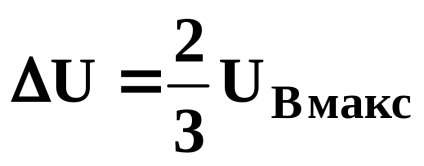
Так як заряди з ємностей здорових фаз переходять на ємність пошкодженої фази через індуктивність трансформатора, то цей процес носить коливальний характер з частотою
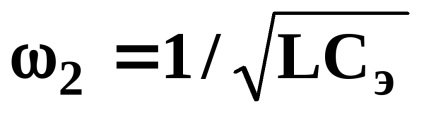
Амплітуда коливань дорівнює різниці між миттєвим значенням вимушеного напруги на пошкодженій фазі безпосередньо після обриву дуги UA (t2) + U і початкової напруги до обриву дуги рівного нулю. У розглянутому прикладі.
На фазі А відбувається характерний сплеск напруги, званий піком гасіння, який наближено дорівнює Uпг 2Uкол = 2 [UA (t2) + U].
Після затухання коливань відбувається повільний підйом напруги з частотою джерела. Одночасно зі зміною напруги, що відновлюється по кривій UA (рис.1.2) відбувається відновлення електричної міцності дугового проміжку по кривим А, Б або В.
Випадок А характерний для невеликих мереж з малою ємністю С, у яких дуга ліквідується протягом одного напівперіоду промислової частоти.
Це мережі 35 кВ при токах замикання на землю Iз = 5 10 А і мережі 6-10 кВ при Iз = 20 30 А.
У разі Б крива відновлення електричної міцності дугового проміжку проходить вище Uпг і перетинається з кривою UA поблизу її максимуму. У цей момент дуга знову загориться, але може знову погаснути при проходженні через нуль високочастотного струму. Дуга матиме перемежовується характер.
У разі В повторне запалювання дуги відбудеться в момент t3 незабаром після гасіння. Запалювання буде супроводжуватися коливальним процесом, але з меншою амплітудою, тому що напруга на здорових фазах в цей момент наблизилося до сталого значення. Імовірність гасіння дуги при другому проходженні струму через нуль буде вище, а зсув нейтралі U менше. Чергова спроба гасіння дуги відбудеться під час наступного проходженні високочастотного струму через нуль. Якщо дуга згасне під час високочастотних коливань, то вона може бути погашена при проходженні через нуль струму промислової частоти. Таким чином у разі В дуга може бути як переміжної, так і стійкою.
Найбільшу небезпеку для ізоляції представляють перемежовуються дуги, причому найбільші перенапруги виникають, коли повторне запалення відбувається приблизно через півперіоду після гасіння дуги. Збільшення напруги в перехідному режимі в порівнянні з першим запалюванням обумовлено зміщенням нейтралі U. Як видно з рис.1.2, в момент t4 збільшується різниця між сталим значенням UAB і напругою на здорової фазі UB + U, що і призводить до збільшення амплітуди вільних коливань.
Для визначення максимальної напруги при n-му запалюванні дуги можна скористатися формулою визначення UB макс. враховуючи, що напруга фази А в момент, що передує запалювання, зростає на величину зсуву нейтралі, що утворився в результаті попереднього гасіння дуги.
Використовуючи цю формулу, розглянемо деякі варіанти поведінки дуги і визначимо граничні значення перенапруг.
1.Дуга гасне при першому проходженні через нуль струму високочастотних коливань і запалюється через півперіоду в момент максимальної напруги на пошкодженій фазі (криві Б і UA на рис.1.2) - теорія Петерсена.
Цей режим ідеалізовано і малоймовірний, проте він дозволяє отримати граничні значення перенапруг.
У табл.1.1 наведені розрахункові значення напруг, отримані по даній теорії при k = 0,2 і d = 0,1.
Як видно з таблиці максимальні перенапруги і зміщення нейтралі ростуть від напівперіоду до напівперіоду, але темп зростання поступово сповільнюється, тому що поряд з процесом накопичення зарядів на ємностях, коли дуга не горить, йде процес стікання зарядів на землю при горінні дуги. Поступово зростання перенапруг припиняється. Граничне значення перенапруг може бути знайдено, прирівнявши Unмакс = U (n-1) макс, і тоді
У розглянутому прикладі Unмакс = 4,26Uф.
За теорією Петерсена напруга на здорових фазах може підвищуватися до 7,5Uф.
Таблиця 1.1. Розрахункові значення напруг в відносних одиницях
2.Експеріменти в мережах і на моделях, проведені Н.Н.Беляковим, показали, що дуга може стати пустим при проходженні через нуль як високочастотного струму, так і струму промислової частоти. Причому спроба гасіння дуги закінчується вдало, якщо пік гасіння не перевищує певного значення. Наприклад, для мереж 6-10 кВ дуга гасне, якщо Uпг 0,4Uф. У свою чергу це умова впливає на зміщення нейтралі, яке повинно бути не більше U = 0,5Uпг + Uф = 1,2Uф. Якщо U> 1,2Uф. то Uпг> 0,4Uф - дуга згасне і тут же загориться знову. Заряди ємностей будуть частково відводитися на землю. При наступному проходженні високочастотного струму через нуль буде ще одна спроба гасіння дуги і так до тих пір поки значення Uпг не стане менше 0,4Uф.
Після цього дуга гасне і може спалахнути лише під впливом напруги, що відновлюється промислової частоти приблизно через півперіоду. Використовуючи формулу для Unмакс. можна знайти максимальне значення перенапруг, якщо підставити в неї таке значення: U = 1,2Uф; UA = UФ sin; UB = Uф sin ( 120). Тоді при = 90
Слід зазначити, що найбільші перенапруги виникають не в момент максимуму напруги на пошкодженій фазі, а дещо раніше, що більш імовірно.
Теорія Белякова дає менші значення перенапруг, ніж теорія Петерсена, крім того по ній напруги наростають не поступово, а при другому запалюванні дуги (через півперіоду). Однак вона носить приватний характер, тому що заснована на експериментах, обмежених певними умовами. За теорією Белякова напруги на здорових фазах можуть підвищуватися до 4Uф.
3. За теорії Петерса-сліпучого дуга гасне при переході через нуль струму промислової частоти і запалюється знову при максимальній напрузі промислової частоти на пошкодженій фазі.
В цьому випадку гасіння дуги відбувається через півперіоду після запалювання, коли вільні коливання затухнуть. При цьому напруги на здорових фазах дорівнюватимуть 1,5Uф. а U = Uф.
Підставивши ці значення в формулу визначення максимальної напруги, отримаємо UВ макс = 1,5Uф + 2Uф (1 k) (1 d) = 1,94Uф.
За теорією Петерса-сліпучого максимальні перенапруги можуть досягати 3,5Uф.
У реальних мережах перенапруги (3 3,2) Uф є граничними. Подібні перенапруги не є небезпечними для ізоляції класу 35 кВ. Однак тривале їх існування може викликати пошкодження ослабленою або забрудненої ізоляції. Крім того, дуга може перекинутися на інші фази. Тому дугове замикання фази на землю має бути ліквідовано можливо швидше.