Особливість арифметичних пристроїв полягає в тому, що двійковим сигналам, двом відомим станам низького і високого рівня приписуються не тільки логічні, але і арифметичні значення 0 і 1 і дії над ними підкоряються законам арифметики.
До арифметичним відносяться пристрої, що виконують арифметичні дії з двійковими числами: додавання, віднімання, множення, ділення, піднесення до степеня, взяття логарифма і т.д. До арифметичним ставляться так само спеціальні пристрої:
для визначення парності (паритету)
для порівнювання двох багаторозрядних чисел (компаратори)
для мажоритарного контролю (кворум - елементи)
Всі арифметичні операції з двійковими числами зводяться до складання: віднімання - це складання двох чисел, одне з яких представлено в зворотному або додатковому коді; множення - це багаторазове складання і зрушення; поділ - це багаторазове віднімання і зрушення. Статечні, логарифмічні та інші складні функції в цифровій електроніці, в ЕОМ обчислюються по наближених формулах, що включає додавання і множення.
Суматор. SUMMER SUMMATOR
Суматор двох однорідних доданків називається полусумматора і позначають HS - HALF SUM - половина суми.
`
P = AB перенесення (переповнення) іноді позначають С або CR від CARRY - перенесення.
Щоб не було плутанини в позначеннях логічних і арифметичних дій при описі арифметичних пристроїв знаком + будемо позначати тільки арифметичну суму, а знаком V - логічну функцію АБО, логічне додавання. знак

При складанні двох багаторозрядних двійкових чисел крім двох входів доданків в суматорі кожного розряду повинен бути ще вхід для перенесення з молодшого розряду. Полусумматор має тільки два входи і значить придатний для підсумовування тільки наймолодшого розряду доданків, і не придатний для підсумовування всіх інших розрядів доданків.
Для складання будь-якого розряду двох доданків з урахуванням перенесення з молодшого розряду призначений однорозрядних повний суматор або просто суматор.
Суматор можна побудувати з двох полусумматора. Перший полусумматор HS1 складає два доданків і виробляє проміжні суму Si 'і перенесення Pi'. Другий полусумматор HS2 підсумовує перенесення з попереднього розряду Pi-1 з проміжною сумою Si-1. в результаті виходить повна сума Si. Перенесення отримуємо за участю двох HS і додаткових логічних елементів АБО.
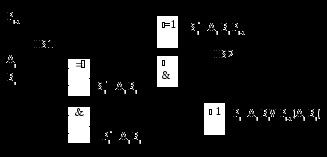



Булеві вирази для Si і Pi після мінімізації і з урахуванням один одного стануть:
Схема SM по цих мінімізованих виразами на логічних елементах І-АБО-НЕ використовується в якості основи в мікросхемах 155 ІМ 1,2,3. тут виходи
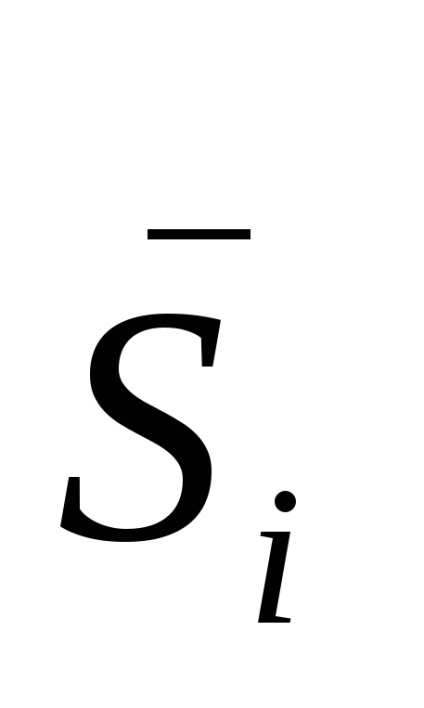
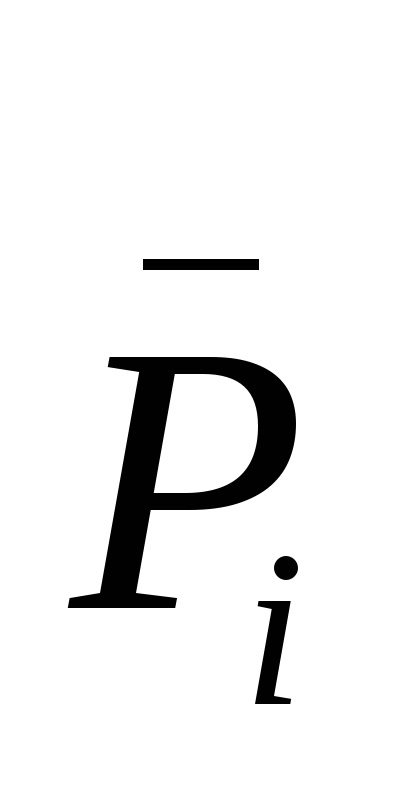

Однорозрядних суматор може бути використаний для підсумовування багаторозрядних двійкових чисел, якщо вони представлені послідовним кодом, в якому молодші розряди слідують раніше старших. У цьому випадку сигнал з виходу переносу подається на вхід перенесення цього ж суматора через ланцюг затримки, що забезпечує зберігання перенесення на час одного такту проходження імпульсів вхідних цифрових доданків. Це самий повільний спосіб підсумовування багаторозрядних чисел, але він найекономічніший по апаратурі.
Паралельне підсумовування з послідовним переносом.
Тут число суматорів дорівнює числу розрядів. Швидкодія обмежена затримкою перенесення, так як формування сигналів суми Sn і перенесення Pn старшого розряду не може відбутися доти, поки сигнал перенесення молодшого розряду не поширився послідовно по всьому ланцюжку.


Паралельне підсумовування з паралельним переносом.
Час, затримки перенесення можна зменшити вводячи паралельний перенос, для чого застосовують схеми прискореного переносу (СУП) '. У цих схемах перенесення кожного розряду виробляється незалежно від перенесення сусіднього молодшого розряду, він формується з доданків даного розряду і з вхідного перенесення всього суматора (в попередньому розряді він подавався на вхід перенесення молодшого розряду).
Для опису роботи суматора з паралельним переносом ввести дві допоміжні функції γ і π:
γ - функція генерації перенесення (CARRY GENERATORION - CRG) γi = Ai Bi; γi = 1Якщо в даному i-тому розряді суматора генерує перенесення, якщо Ai = Bi = 1 і γi = 0 в усіх інших випадках.
π - функція прозорості мул поширення (CARRY PROPOGATION - CRPP), π = AiVBi, іноді прінімаютπ = Ai

Процес формування прискореного перенесення описується рівнянням
На практиці функції γ і π це проміжні сигнали розрядів схеми суматора, які використовують для формування сигналу паралельного перенесення всього суматора.
У пристроях дискретної техніки операція віднімання зазвичай замінюється складанням зменшуваного з від'ємником, коли останнім представлено в додатковому коді.
Нехай треба отримати різницю двох чисел A-B, де A і B - hfphzlyst двійкові числа.
B + Bдоп = B +
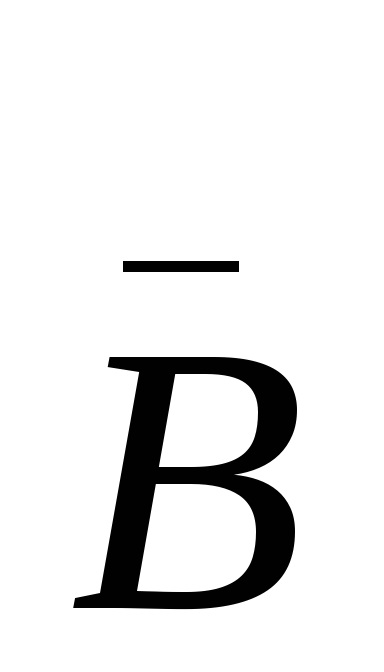
n розрядів n + 1 розряд
B = 1000 ... 0 -Bдоп = 111 ... 1 + 1
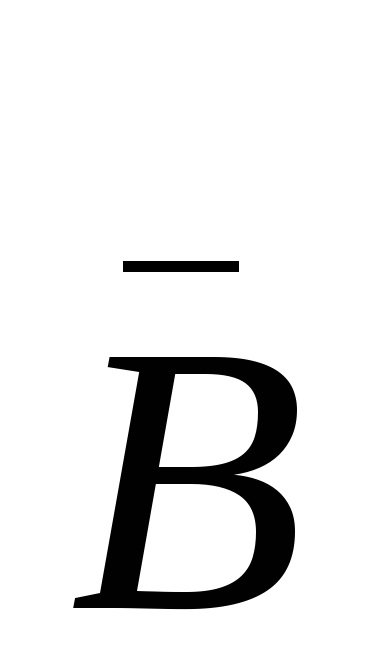
n розрядів n + 1 розряд
A-B = A-1000 ... 1 +
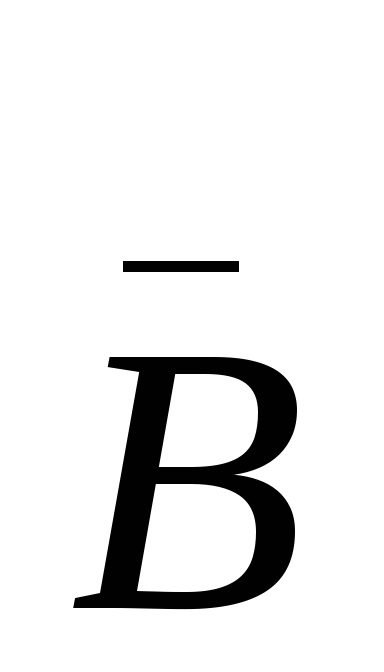
Це означає що для вирахування двох чисел досить провести їх складання, якщо при цьому від'ємник представлено в додатковому коді.
При такому відніманні якщо різниця позитивна, тобто A> B, то ця різниця буде представлена в прямому коді, а в розряді, старшому старшого, тобто в n + 1разряде утворюється 1, якою можна знехтувати.
Якщо при такому відніманні різниця негативна, тобто A Множення і ділення двійкових чисел. Так як часткове твір многоразрядного числа на 1 одно цього числа, а множення на 0 дає нулі у всіх розрядах, то операція множення зводиться до операцій зсуву і складання часткових творів.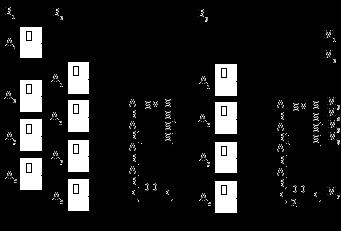

Схема помножувача четирёхразрядного числа A4A3A2A1 на трёхразрядное число B3B2B1, реалізовано на мікросхемах типу К155ІМ3. Семіразрядний твір M7M6M5M4M3M2M1 на виході помножувача формується за рахунок паралельного множення множимо A на кожен розряд множника B логічними елементами 2І і складання проміжних творів із зсувом на один розряд - суматорами SM DD1 і DD2.
Застосування логічних елементів І для виконання арифметичної операції множення в даному випадку допустимо, оскільки в рамках одного розряду і арифметичне множення і логічне (функції І, сполучення) підкоряються загальним правилам.
Двійкове ділення до наступних операцій: віднімання дільника з діленого, зрушення дільника на один розряд, порівняно отриманого залишку з подільником, якщо залишок менше дільника, то зрушення дільника ще на один розряд, знову порівнянні подільника із залишком, якщо залишок більше дільника, то з нього віднімається дільник, потім знову слід зрушення дільника, знову порівняння, так до тих пір, поки після зсуву дільника його молодший розряд зрівняється з молодшим розрядом діленого. У тих розрядах, де порівняння подільника із залишком показувало, що залишок менше дільника, в цей розряд результату ділення - приватного - записується нуль, в інших розрядах - 1. Отже, розподіл зводиться до віднімання, зсуву і порівнянню.
Компаратор (схема порівняння) COMPARУ - порівнювати, звіряти.
Порівнює два багаторозрядних числа A і B за величиною. Зазвичай має три виходи. A
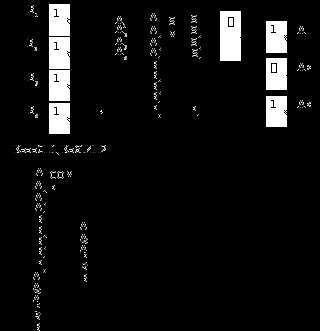

Якщо згадати розділ про вирахування двійкових чисел, то стане зрозуміло, чому з сигналу перенесення виходять сигнали A> B і A

Практично будь-який канал передачі даних, або будь-який ЗУ, якщо вони не мають будь-якого більш сильного методу контролю, захищені контролю за парності, за паритетом (PARITY - відповідність) на n вхідному елементі
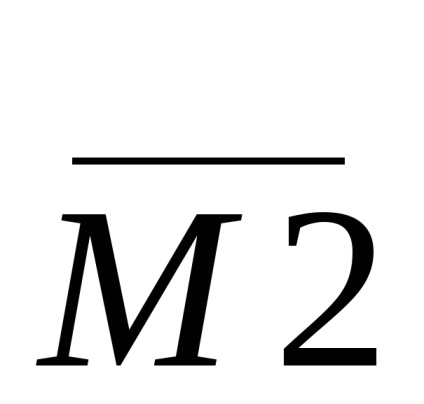
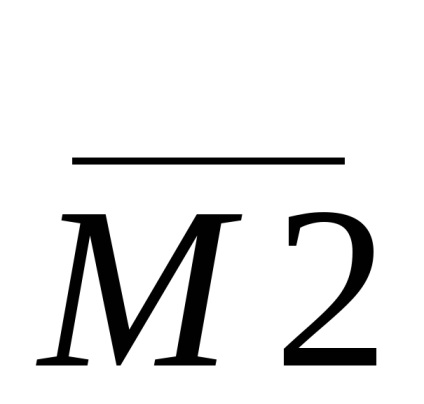
Це дає можливість виключить невірні дані, вимагати повторну передачу і т.п.
Мікросхеми для контролю парності крім n розрядного елемента M2, який виконує піраміди 2х входові елементів = 1 (виключають АБО) (до речі, для двухвходових M2 еквівалентно = 1), доповнюють схемами вибору ознаки контролю: по парності або по непарності.


Вузли мажоритарного контролю.
Вони є найпростішими за змістом схемами, що дозволяють не тільки визначати, а й виправляти помилки, що відбулися при передачі або обробки даних. При цьому використовуються три канали - при передачі, або три блоки - при обробці даних; вихідні дані з них надходять на вузол мажоритарного контролю (вузол мажорірованія, кворум-елемент), який формує з них один вихідний сигнал за принципом голосування "два з трьох", вихідний сигнал дорівнює лог.1 якщо на двох або трьох виходах лог 1. В склад вузла мажоритарного контролю зазвичай вводять елемент, що дозволяє оцінити номер відмовив (незгодного з іншим) каналу або блоку. AER - ADRESS ERROR. MSB - MOST SIGNIFICAT BTT - найбільш значимий розділ. LSB - LEAST BIT - найбільш значимий розряд двійкового коду, що позначає номер відмовив каналу.
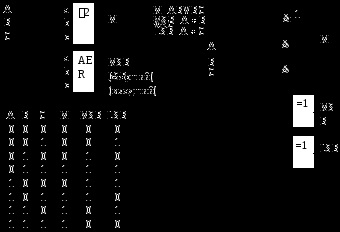

Арифметико-логічні пристрої ALU-ARITHMETIC and LOGIK UNIT
У мікропроцесорній техніці АЛУ є базовими елементами. При М = Н (високий) мікросхема виконує логічні функції від четирехразрядних вхідних змінних А і В. Вибір конкретної функції з 16 можливих задається набором вхідних сигналів SO ... S3:
При М = L (низький) АЛУ ІП3 виробляє арифметичні операції над чотирирозрядний двійковими числами А і В. Набір (комбінація) вхідних сигналів SO ... S3 визначає одну з 16 можливих операцій:
Тут Асдв одно А, кожен розряд якого зміщений в напрямку більш високого розряду.
Cn - вхід, а Cntu - вихід переносу
G і Р - виходи функцій γ генерації перенесення і π - прозорість перенесення для підключення схеми прискореного переносу К155 ІП4.

