У цій статті розглянемо кілька нестандартний і іноді істотно спрощує вирішення метод векторних діаграм.
Всі рівняння кінематики в хорошому підручнику фізики будуть приведені у векторному вигляді. Але, вирішуючи завдання, ми зазвичай записуємо їх же в проекціях на осі координат і отримуємо замість одного витонченого рівняння велику систему. Це корисно або в найпростіших випадках, або в окремих трудомістких завданнях. Існує великий клас завдань, в якому такий підхід виявиться неоптимальним, а допомогти зможе геометричний опис. Оскільки у цих завдань «правильним» методом рішення виходить дуже красивим і досить коротким, вони часто з'являються на олімпіадах різного рівня. Будемо розглядати випадок вільного падіння тіл в полі тяжіння за відсутності опору повітря. Схематично він може бути зображений таким чином:
Основні співвідношення кінематики, записані в векторному вигляді:
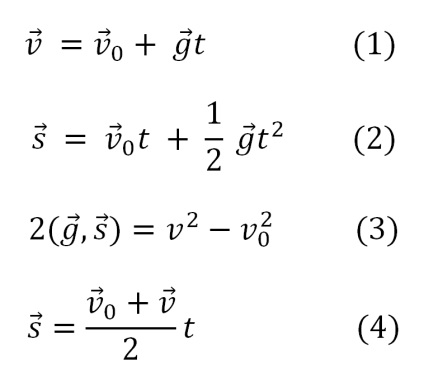
Методом використовуються два ключових векторних трикутника: швидкостей і переміщень:
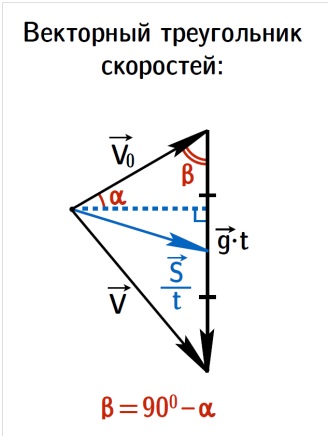
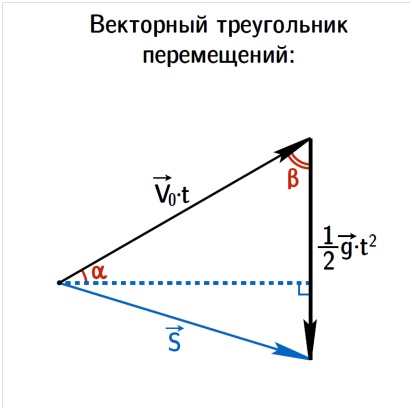
Побудуємо векторний трикутник швидкостей:
Відкладемо вектор v0 під якимось початковим кутом α до горизонту, до його кінця прірісуем вектор g t, спрямований вертикально вниз. Сума цих двох векторів по рівнянню (1) дасть нам вектор v.
Щоб побудувати векторний трикутник переміщень, паралельно v0 відкладемо вектор v0 t. До його кінця додамо вектор. Відповідно до рівняння (2), отримаємо вектор s як їх суму.
Подивимося на малюнок уважніше: висота, опущена до вертикальної сторони, - зміщення тіла по горизонталі або, як її зазвичай називають, дальність польоту L. α - як і раніше, кут кидка до горизонту. Катет, протилежні кутку α, - зміщення по вертикалі h.
Повернемося до трикутника швидкостей. З (2) випливає:
Значить, - медіана, проведена до вертикальної сторони трикутника переміщень. Це відповідає і рівняння (4), де відповідає медіані трикутника, побудованого на векторах швидкостей.
З міркувань подібності і порівнюючи два трикутника, отримуємо, що висота, проведена до тієї ж сторони, дорівнює, а катет верхнього прямокутного трикутника, протилежний куту α, дорівнює.
Таким чином, нам вдалося об'єднати два ключових трикутника і висловити основні співвідношення кінематики геометрично. Виділимо деякі окремі випадки і виникають властивості трикутників:
Якщо v0⊥v. то трикутник швидкостей виходить прямокутним, а значить, медіана дорівнює половині гіпотенузи:.
Якщо v0⊥v. то трикутник швидкостей складається з двох рівнобедрених трикутників, отже, швидкість v0 спрямована по бісектрисі кута, утвореного вертикаллю і вектором s.
Площа трикутника швидкостей можна виразити як.
Для прикладу розберемо завдання:
З поверхні землі під кутом до горизонту кидають камінь. Через час τ він падає на поверхню пагорба, причому зі швидкістю, перпендикулярної початкової. Чому дорівнює відстань між точками кидка і приземлення? Опором повітря знехтувати.
Розглянемо трикутник швидкостей. Швидкості на початку і в кінці польоту перпендикулярні ⇒ маємо прямокутний трикутник. Медіана дорівнює половині гіпотенузи ⇒.
Пропонуємо вирішити такі завдання (джерела вказані поруч з номером).
1. Козел, Слободянін 9.62
Кот Леопольд сидів у краї даху. Два бешкетних мишеняти вистрілили в нього каменем з рогатки. Камінь, описавши дугу, впав біля ніг кота через час τ = 1 c. На якій відстані від мишей знаходився кіт Леопольд, якщо вектори швидкостей каменю в момент пострілу і в момент падіння були взаємно перпендикулярні?
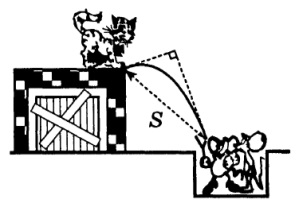
2. Козел, Слободянін 9.71
Кот Леопольд стояв біля краю даху сараю. Два бешкетних мишеняти вистрілили в нього каменем з рогатки. Однак камінь, описавши дугу, через t1 = 1,2 с пружно відбився від похилого ската даху сараю у самих лап кота і через t2 = 1,0 с потрапив в лапу того, хто стріляв мишеняти. На якій відстані s від мишей знаходився кіт Леопольд?
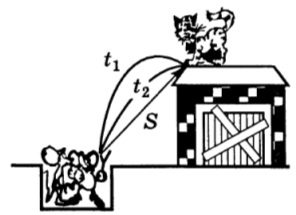
3. Савченко 1.3.17
У прямокутної коробці, пружно вдаряючись об дно і праву стінку, по одній траєкторії туди і назад стрибає кульку. Проміжок часу між ударами об дно і стінку дорівнює Δt. Дно коробки утворює кут α з горизонтом. Знайдіть швидкості кульки відразу ж після ударів.
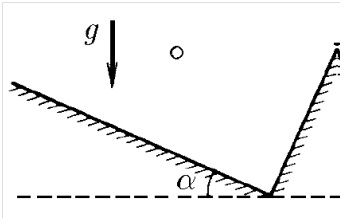
4. Савченко 1.3.10
Качка летіла по горизонтальній прямій з постійною швидкістю u. У неї кинув камінь недосвідчений «мисливець», причому кидок був зроблений без попередження, тобто в момент кидка швидкість каменю v була спрямована якраз на качку під кутом α до горизонту. На якій висоті летіла качка, якщо камінь все ж потрапив в неї?