Історичні відомості про правильні многогранниках ............... .. ... .9
Правильні багатогранники навколо нас ..................................... 14
Тема «Багатогранники» одна з основних в традиційному курсі шкільної геометрії. Вони складають, можна сказати, центральний предмет стереометрії. Вивчення паралельних і перпендикулярних прямих і площин, двогранні кутів і інше, так само як введення векторів і координат, - все це тільки почала стереометрії, підготовка засобів для дослідження її більш змістовних об'єктів - головним чином тіл і поверхонь.
Центральна роль багатогранників визначається перш за все тим, що багато результати, пов'язані з іншим тілам, виходять виходячи з відповідних результатів для багатогранників; Досить згадати визначення об'ємів тіл і площ поверхонь шляхом граничного переходу від багатогранників.
Крім того, багатогранники самі по собі представляють надзвичайно змістовний предмет дослідження, виділяючись серед всіх тіл багатьма цікавими властивостями, спеціально до них відносяться теоремами і завданнями. Можна, наприклад, згадати теорему Ейлера про кількість граней, ребер і вершин, симетрію правильних багатогранників, питання про заповнення простору многогранниками і ін.
Многогранників має бути приділено в шкільному курсі більше уваги ще й тому, що вони дають особливо багатий матеріал для розвитку просторових уявлень, для розвитку того з'єднання живого просторової уяви з суворою логікою, яке становить сутність геометрії. Уже найпростіші факти, що стосуються багатогранників, вимагають такого з'єднання, яке виявляється при цьому не зовсім легкою справою. Навіть такий простий факт, як перетин діагоналей паралелепіпеда в одній точці, вимагає зусиль уяви, щоб його побачити наочно, і потребує строгого доказу.
Більш того, використання багатогранників з самого початку вивчення стереометрії служить різним дидактичним цілям. На многогранниках зручно демонструвати взаємне розташування прямих і площин в просторі, показувати застосування ознак паралельності і перпендикулярності прямих і площин в просторі. Ілюстрація перших теорем стереометрії на конкретних моделях підвищує інтерес учнів до предмету.
Також однією з основних задач навчання математики є розвиток в учнів абстрактного мислення. Цій меті значною мірою сприяє застосування наочних посібників, причому не тільки в молодших класах, але і в старших. Широкі можливості для реалізації цієї мети надає тема «Багатогранники», зокрема, самостійне виготовлення учнями наочних посібників. В процесі виготовлення моделей багатогранників, крім теоретичних знань і навичок, учні закріплюють сформувалися нові поняття за допомогою креслення і фактичного вирішення завдань на побудову. При самостійному виготовленні моделей образ створюється по частинах, в силу цього з ними можна робити різні маніпуляції. При цьому всі їх властивості та особливості легко пізнаються і міцно закріплюються в пам'яті учнів.
Багатогранник - це геометричне тіло, обмежене з усіх боків плоскими багатокутниками, званими гранями.
Сторони граней - ребра багатогранника, а кінці ребер - вершини багатогранника. За кількістю граней розрізняють чотиригранник, пятіграннікі і т. Д.
Багатогранник називається опуклим, якщо він весь розташований по одну сторону від площини. кожної з його граней.
Опуклий багатогранник називається правильним, якщо всі його грані - однакові правильні багатокутники, в кожній вершині сходиться одне і те ж число ребер, а сусідні грані утворюють рівні кути.
На малюнку зображено тетраедр, гексаедр, октаедр, додекаедр і ікосаедр. Їх форма - зразок досконалості! А чому правильні багатогранники отримали саме таку назву? Якими особливостями вони володіють? Як виготовити модель будь-якого правильного багатогранника? Де можна зустріти ці дивовижні тіла?
Відповісти на ці та інші питання: мета даної роботи.
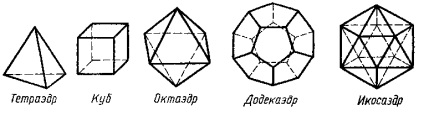
Всі правильні багатогранники мають різну кількість граней і назви отримали з цього числа.
Тетраедр (від. Тетра "- чотири і грецького. Hedra" - грань) складено з 4-х правильних трикутників, в кожній його вершині сходяться 3 ребра.
Гексаедр (від грецького. Гекса "- шість і. Hedra" - грань) має 6 квадратних граней, в кожній його вершині сходяться 3 ребра.
Гексаедр більше відомий як куб (від латинського. Cubus "; від грецького. Kubos".
Октаедр (від грецького okto - вісім і hedra - грань) має 8 граней (трикутних), в кожній вершині сходяться 4 ребра.
Додекаедр (від грецького dodeka - дванадцять і hedra - грань) має 12 граней (п'ятикутних), в кожній вершині сходяться 3 ребра.
Ікосаедр (від грецького eikosi - двадцять і hedra - грань) має 20 граней (трикутних), в кожній вершині сходиться 5 ребер. (5, с.267-269)
Виявляється, що правильних багатогранників рівно п'ять - ні більше ні менше. Адже для того, щоб отримати який-небудь правильний багатогранник, в кожній вершині, згідно з його визначенням, має сходитися однакову кількість граней, кожна з яких є правильним багатокутником.
Сума плоских кутів багатогранного кута повинна бути менше 360 о. інакше ніякої багатогранної поверхні не вийде. Перебираючи можливі цілі рішення нерівностей: 60к
Правильні багатогранники навколо нас.
У книзі німецького біолога початку нашого століття Е. Геккеля "Краса форм у природі" можна прочитати такі рядки: "Природа вигодовує на своєму лоні невичерпна кількість дивних створінь, які по красі і різноманітності далеко перевершують все створені мистецтвом людини форми". Так, наприклад, одноклітинні організми феодаріі, мають форму ікосаедра.
Цікаво й те, що саме ікосаедр опинився в центрі уваги біологів в їх спорах щодо форми вірусів. Вірус не може бути абсолютно круглим, як вважалося раніше. Щоб встановити його форму, брали різні багатогранники, направляли на них світло під тими ж кутами, що і потік атомів на вірус. Виявилося, що тільки один багатогранник дає точно таку ж тінь - ікосаедр. Його геометричні властивості, про які говорилося вище, дозволяють економити генетичну інформацію. Правильні багатогранники - найвигідніші фігури. І природа цим широко користується. Кристали деяких знайомих нам речовин мають форму правильних багатогранників. Так, куб передає форму кристалів кухонної солі NaCl, монокристал алюмінієво-калієвих квасцов має форму октаедра, кристал сірчистого колчедану FeS має форму додекаедра, сурьменістий сірчанокислий натрій - тетраедра, бор - ікосаедра.
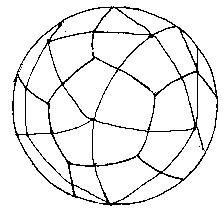
Якщо нанести на глобус вогнища найбільш великих і примітних культур і цивілізацій Стародавнього світу, можна помітити закономірність в їх розташуванні щодо географічних полюсів і екватора планети. Багато поклади корисних копалин тягнуться вздовж ікосаедрово-додекаедровой сітки. Ще більш дивні речі відбуваються в місцях перетину цих ребер: тут розташовуються осередки найдавніших культур і цивілізацій: Перу, Північна Монголія, Гаїті, Обская культура та інші. У цих точках спостерігаються максимуми і мінімуми атмосферного тиску, гігантські завихрення Світового океану, тут шотландське озеро Лох-Несс, Бермудський трикутник. Подальші дослідження Землі, можливо, визначать відношення до цієї красивої наукової гіпотези, в якій, як видно, правильні багатогранники займають важливе місце. (2, с.2)
Дослідницька робота була цікавою і різноманітною і змусила зрозуміти, що світ, що оточує нас, підпорядковується законам геометрії.
В рамках роботи над рефератом була вивчена література по темі, виявлено особливості правильних багатогранників, виготовлені креслення, розгортки, моделі правильних багатогранників.
Багатогранник в тривимірному просторі, сукупність кінцевого числа плоских багатокутників, така, що кожна сторона будь-якого з багатокутників є одночасно сторона іншого (але тільки одного), званого суміжним з першим (по цій стороні); від будь-якого з багатокутників, складових Багатогранник. можна дійти до будь-якого з них, переходячи до суміжного з ним, а від цього, в свою чергу, - до суміжного з ним, і т. д. Ці багатокутники називаються гранями, їх сторони - ребрами, а їх вершини - вершинами багатогранників.
Світ наш сповнений симетрії. З найдавніших часів з нею пов'язані наші уявлення про красу. Напевно, цим пояснюється неминущий інтерес людини до правильних многогранників - дивним символам симетрії, що вабили увагу безлічі видатних мислителів, від Платона і Евкліда до Ейлера і Коші.
Форма першоелемента Землі - куб, Повітря - октаедр, Вогню - тетраедр, Води - ікосаедр, а всьому світу творець надав форму п'ятикутного додекаедру. Про те, що Земля має форму кулі, вчили Піфагорійці. За Піфагору, існує 5 тілесних фігур: вища божество саме побудувало Всесвіт на підставі геометричної форми додекаедра. Земля подібна Всесвіту, і у Платона Земля - теж додекаедр.
Грецька математика, в якій вперше з'явилася теорія багатогранників, розвивалася під великим впливом знаменитого мислителя Платона.
Платон (427-347 до н.е.) - великий давньогрецький філософ, засновник Академії і родоначальник традиції платонізму. Одним з істотних рис його вчення є розгляд ідеальних об'єктів - абстракцій. Математика, взявши на озброєння ідеї Платона, з часів Евкліда вивчає саме абстрактні, ідеальні об'єкти. Однак і сам Платон, і багато стародавніх математики вкладали в термін ідеальний не тільки зміст абстрактний, а й сенс найкращий. Відповідно до традиції, що йде від стародавніх математиків, серед всіх багатогранників кращі ті, які мають своїми гранями правильні багатокутники.
Теорія багатогранників - один з цікавих і яскравих розділів математики. У представленому рефераті було розглянуто тільки одна частина цієї теорії. З правильних багатогранників - платонових тел - можна отримати так звані напівправильні багатогранники, або архимедови тіла, гранями яких є також правильні, але різнойменні багатокутники, а також зоряні правильні тіла.
1.Дорофеев Г.В. Петерсон Л.Г. Математика. 6 клас. Частина 3 - М: Баласс, 1988.