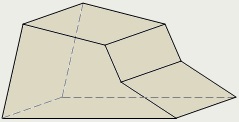
Деякі просторові фігури, що вивчаються в стереометрії, називають тілами або геометричними тілами. Наочно тіло треба уявляти собі як частину простору, зайняту фізичним тілом і обмежену поверхнею.
Багатогранником називається геометричне тіло, поверхня якого складається з кінцевого числа плоских багатокутників.
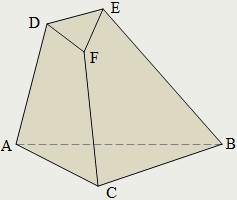
Опуклим називається багатогранник, якщо він розташований по одну сторону площині, проведеної через будь-який багатокутник, який утворює поверхню даного багатогранника.
Багатокутники, складові поверхню багатогранника, називаються його гранями; боку багатокутників - ребрами; вершини - вершинами многогранника:
ABC. DEF. ABED. BCFE. ACFD - межі;
AB. BC. AC. DE. EF. DF. AD. BE. CF - ребра;
A. B. C. D. E. F - вершини багатогранника ABCDEF.
Теорема Ейлера для багатогранників.
Якщо V - число вершин опуклого багатогранника, R - число його ребер і G - число граней, то вірно рівність:
V - R + G = 2.
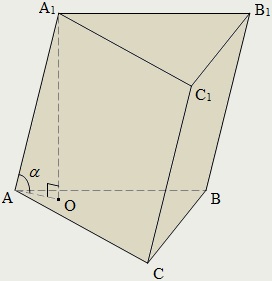
Призмою називається багатогранник, що складається з двох плоских багатокутників, які лежать в різних площинах і суміщаються паралельним перенесенням, та всіх відрізків, що з'єднують відповідні точки цих многокутників. Багатокутники, про які йшла мова, називаються підставами призми, а відрізки, що з'єднують їх відповідні вершини - бічними ребрами призми.
Підстави призми рівні і лежать в паралельних площинах.
Бічні ребра призми рівні і паралельні.
Поверхня призми складається з двох підстав і бічної поверхні.
Бічна поверхня будь-призми складається з паралелограмів, у кожного з яких дві сторони є відповідними сторонами підстав, а дві інші - сусідніми бічними ребрами.
Висотою призми називається будь-який з перпендикулярів, проведених з точки одного підстави до площини іншої основи призми.
Призма називається п -угольной, якщо її основа - п -угольнік.
A1 Про - висота призми;
α - кут нахилу бічного ребра до основи призми.
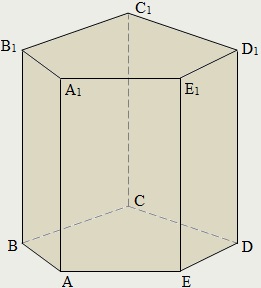
Призма називається прямою, якщо її ребра перпендикулярні площинах підстав. В іншому випадку призма називається похилою.
Бічні грані прямої призми - прямокутники.
Бічне ребро прямої призми є її заввишки.
Бічна поверхня прямої призми дорівнює добутку периметра основи на висоту призми:
Пряма призма називається правильною, якщо її заснування є правильними багатокутниками.
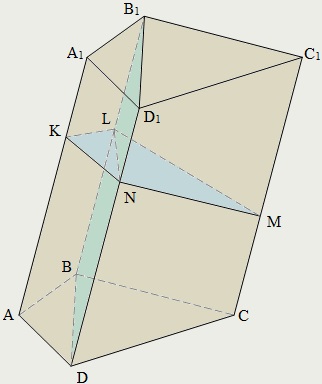
Перетину призми площинами, паралельними бічним ребрам, є паралелограма. Зокрема, паралелограма є діагональні перерізи. Це перетину площинами, що проходять, через два бічних ребра, які не належать одній грані:
ВВ1 D1 D - діагональна розтин.
Якщо в довільній похилій призмі провести розтин, перпендикулярний бічним ребрам і перетинає всі бічні ребра, і площа цього перерізу позначити S⊥. а периметр - Р⊥. тоді:
- для бічної поверхні призми вірно:
- для обсягу призми вірно:
У прямій призмі:
У будь-якій призмі площа повної поверхні вважається як сума площі бічної поверхні і подвоєної площі підстави:
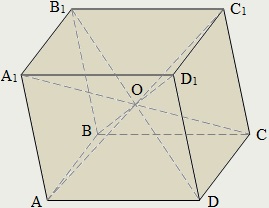
Призма, в основі якої лежить паралелограм, називається параллелепипедом.
У паралелепіпеда всі грані - паралелограми.
Грані паралелепіпеда, що не мають спільних вершин, називаються протилежними.
У паралелепіпеда протилежні грані паралельні і рівні.
Діагоналлю паралелепіпеда, як і багатогранника взагалі, називається відрізок, що з'єднує вершини паралелепіпеда, що не лежать в одній його грані.
Діагоналі паралелепіпеда перетинаються в одній точці і точкою перетину діляться навпіл.
Точка перетину діагоналей паралелепіпеда є його центром симетрії.
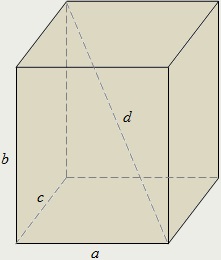
Прямокутним параллелепипедом називається такий прямий паралелепіпед, в основі якого лежить прямокутник.
Всі грані прямокутного паралелепіпеда є прямокутниками.
Довжини ребер прямокутного паралелепіпеда, що виходять з однієї вершини, називаються його вимірами або лінійними розмірами.
У прямокутного паралелепіпеда три виміри.
У прямокутному паралелепіпеді квадрат будь-діагоналі дорівнює сумі квадратів трьох його вимірів:
У прямокутному паралелепіпеді вірно:
- для площі повної поверхні:
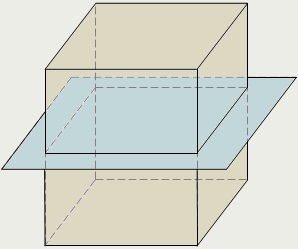
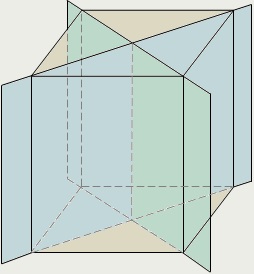
У прямокутному паралелепіпеді, як і у всякому параллелепипеде, є центр симетрії - точка перетину його діагоналей. У нього є також три площини симетрії, що проходять через центр симетрії паралельно парам протилежних граней. На першому малюнку, наведеному вище, показана одна з таких площин. Вона проходить через середини чотирьох паралельних ребер паралелепіпеда.
Якщо у паралелепіпеда всі лінійні розміри різні, то у нього немає інших площин симетрії, крім трьох названих.
Якщо ж у паралелепіпеда два лінійних розміру рівні, тобто він є правильною чотирикутної призмою, то у нього є ще дві площини симетрії. Це площині діагональних перетинів, показані на другому малюнку.
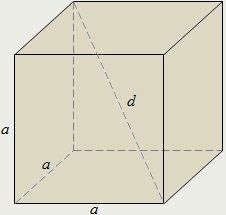
Прямокутний паралелепіпед, у якого всі три виміри рівні, називається кубом.
Діагональ куба в квадратний корінь з трьох разів більше його боку:
- для площі повної поверхні:
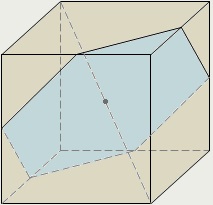
Чотири перетину куба є правильними шестикутниками (одне з них показано на малюнку) - ці перетину проходять через центр куба перпендикулярно чотирьом його діагоналях.
У куба дев'ять площин симетрії:
- три з них, проходячи через середини чотирьох паралельних ребер куба, дають в перетинах квадрати;
- інші шість - це все площині діагональних перетинів куба.
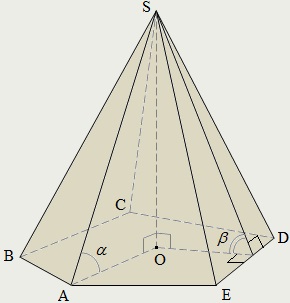
Пірамідою (наприклад, SABCDE) називається багатогранник, який складається з плоского багатокутника (п'ятикутник ABCDE) - основи піраміди, точки (S), що не лежить в площині підстави, - вершини піраміди і всіх відрізків, що з'єднують вершину піраміди з точками основи.
Відрізки (SA. SB. SC. SD. SE), що з'єднують вершину піраміди з вершинами основи, називаються бічними ребрами.
Поверхня піраміди складається з підстави (п'ятикутник ABCDE) і бічних граней. Кожна бічна грань - трикутник. Однією з його вершин є вершина піраміди, а протилежною стороною - сторона основи піраміди:
δSAB. δSBC. δSCD. δSDE. δSEA - бічні грані.
Бічною поверхнею піраміди називається сума площ її бічних граней.
Висотою піраміди (SО) називається перпендикуляр, проведений з вершини піраміди до площини підстави.
Піраміда називається n -угольной, якщо її підставою є n -угольнік. Трикутна піраміда називається також тетраедром.
α - кут нахилу бічного ребра SA піраміди до площини її основи;
β - кут нахилу бічної грані (SED) піраміди до площини її основи.
Підстава висоти піраміди є центром кола, описаного навколо основи піраміди, тоді і тільки тоді, коли виконується одна з умов:
- всі бічні ребра рівні;
- бічні ребра утворюють з площиною основи рівні кути;
- бічні ребра утворюють рівні кути з висотою піраміди.
Підстава висоти піраміди є центром кола, вписаного в основу піраміди, тоді і тільки тоді, коли виконується одна з умов:
- бічні грані нахилені до площини основи під одним кутом;
- висоти бічних граней рівні;
- бічні грані утворюють рівні кути з висотою піраміди.
Обсяг піраміди дорівнює третині добутку площі підстави на висоту піраміди:
V = 1/3 · Sосн h.
Площа повної поверхні будь-якої піраміди дорівнює сумі площ бічної поверхні і підстави:
Перетину піраміди площинами, що проходять через її вершину, є трикутники. Зокрема, трикутниками є діагональні перерізи. Це перетину площинами, що проходять через два несоседних бічних ребра піраміди.
Давно збирався і ось, нарешті! Приблизно так виглядає історія нашої групи ВКонтакте. Сумніви в необхідності її існування відкинуті, і перші матеріали спільноти вже викладені.
Розширено функціональні можливості головного меню.