Багатоконтурна система зворотного зв'язку.
Розмикання багатоконтурною системи зворотного зв'язку з метою отримання передавальної функції можна робити в довільному місці.
Розмикання b / a на вході першої ланки (для отримання головної передавальної функції):
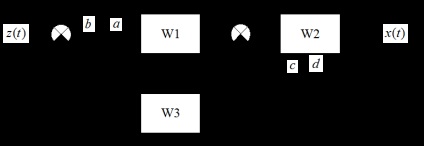
Передавальна функція (головна):
.
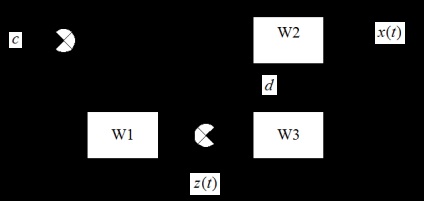
.
Передавальні функції різні. Проте, характеристичні рівняння замкнутої системи однакові:
,
.
Таким чином, для визначення стійкості, можна користуватися функцією передачі системи, отриманої відстань між вихідної системи в довільній точці. Однак тільки головна передавальна функція пов'язана з функцією передачі замкнутої системи відомим співвідношенням:
.
З тієї обставини, що при дослідженні стійкості замкнутої системи нас цікавить тільки характеристичне рівняння
,
випливає, що для розрахунку стійкості може бути використана перетворена передавальна функція
,
де - довільний поліном ступеня меншою, ніж ступінь полінома, тому що
.
Багатовимірні системи регулювання [1].
До багатовимірним відносяться системи, що мають кілька регульованих величин:
, ().
Багатовимірний об'єкт управління описується системою рівнянь, зазвичай подається в матричної формі:
, , .
Тут u. f - керуючі і впливи (вектори).
Рівняння руху в матричної формі:
.
, ,
- квадратна і прямокутні матриці операторних коефіцієнтів.
Для зображень по Лапласа (при нульових початкових умовах):
.
Тут,, - матриці-стовпці зображень регульованих величин, керуючих величин і збурень.
Якщо визначник, то існує обернена матриця. Помноживши вихідне рівняння зліва на отримаємо:
- матриці передавальних функцій об'єкта для керуючих величин і збурень.
Шляхом знаходження зворотного перетворення Лапласа для кожного елемента матриць передавальних функцій об'єкта виходить так звана матриця Коші (матриця вагових функцій). Наприклад, для керуючих впливів
.
Якщо в момент часу на всі входи надходять керуючі впливу, де, то зміна j-тої регульованої величини записується за допомогою інтеграла Дюамеля-Карстоном:
.
На малюнку нижче зображено структурну схему замкнутої багатовимірної системи автоматичного регулювання. Вона в точності така ж, як схема одновимірної системи, тільки g, x, u, y, f тут вектори, а,, - матриці.
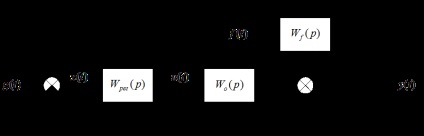
Матриця передавальних функцій розімкнутої по всіх каналах системи:
.
Характеристична матриця системи - квадратна матриця розміром, E - одинична матриця:
.
Характеристичне рівняння - визначник характеристичної матриці:
.
Матриці передавальних функцій замкнутої системи, замкненої системи помилково і замкнутої системи по збурень:
, , .
Стійкість двомірної системи з антисиметричного зв'язками.
Структурна схема двоканальної системи стеження:
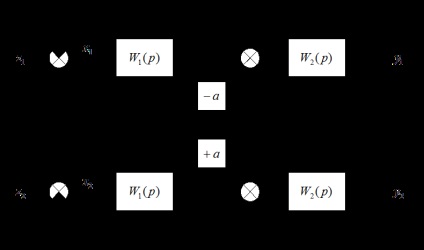
Зв'язок вихідних (регульованих) величин з помилками:
.
.
.
.
Дослідження стійкості зводиться до розгляду двох рівнянь:
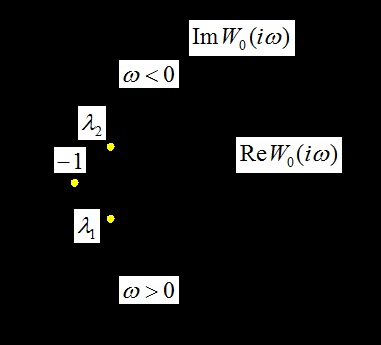
Тут може бути використаний критерій Найквіста, але замість точки комплексної площини (), яка відповідає звичайній запису характеристичного рівняння, необхідно розглядати дві точки, відповідні комплексним числам і.
Замкнута система буде стійкою, якщо АФХ стійкого в розімкнутому стані одного ізольованого каналу не буде охоплювати точок і.
Коливальна межа стійкості матиме місце, якщо виконується одна з рівності або.
Зауважимо, що при обидві точки і стягуються в точку, що відповідає звичайній формулюванні критерію Найквіста.
Інший метод розрахунку стійкості двомірної системи.
Введемо,,. Були співвідношення:
.
Помножимо друга рівність на i і складемо:
.
Тут - еквівалентна передатна функція розімкнутої двомірної системи, - кут повороту передавальної функції за годинниковою стрілкою, - коефіцієнт збільшення модуля.
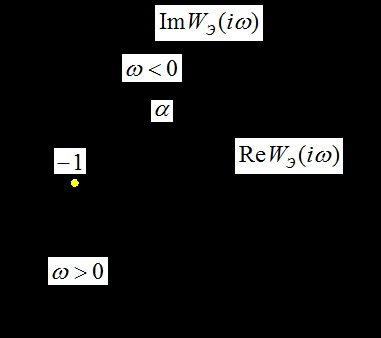
Коливальна межа стійкості:, що зводиться до
.
Це узгоджується з першим методом розрахунку стійкості.