Правила алгебри логіки дозволяють перетворити логічну функцію до вигляду, зручного для реалізації у вигляді логічного пристрою.
Наприклад, задана функція
Для реалізації функції в даному виді потрібно два інвертора НЕ, три трехвходових елемента 3І, один трехвходовий елемент 3ІЛІ:
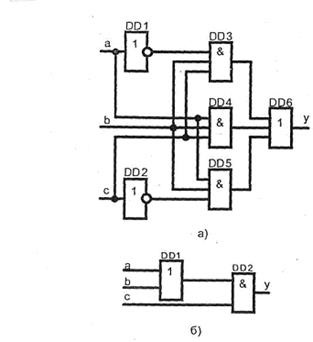
Проведемо еквівалентні перетворення на підставі правил (6), (13), (19)
Очевидно, що після перетворення функція (22) було досягнуто значного спрощення (23). Для її реалізації досить мати один двовходовий елемент 2И, один двовходовий елемент 2ИЛИ (рис. Б). Обидві схеми (рис. А, б) дозволяють реалізувати одну і ту ж функцію у.
При розгляді законів булевої алгебри вико-валися тільки три елементарні функції (НЕ, І, АБО). Всього ж існує 4 функції однієї змінної та 16 функцій двох змінних. Раніше зазначалося, що за допомогою на-гою елементарних функцій можна побудувати будь-яку складну логічну функцію.
Определеніе.Функціонально повна система (базис) - сукупність логічних елементів, яка дозволяє реалізувати будь-яку логічну схему довільної складності.
Для побудови складної логічної функції немає необхідності використовувати всі елементарні функції. Припустимо обмежити набір елементарних функцій, виключаючи з нього ті елементи, які можна виразити через інші. Послідовно виключаючи з базису функції, отримують мінімальний базис.
Визначення. Під мінімальним базисом розуміють такий набір функцій, виключення з якого будь-який функції перетворює повну систему в неповну.
Можуть бути різні базиси, що відрізняються один від одного числом що входять в них функцій і видом цих функцій. Вибір того чи іншого базису для побудови логічних пристроїв обумовлений тим, наскільки економічно вигідно і просто виконати елементи, технічно реалізують входять в базис функції, і все логічне пристрій в цілому.
Через три логічні функції інверсії (НЕ), кон'юнкції (І), диз'юнкції (АБО) можна виразити будь-яку елементарну функцію і побудувати будь-яке складне логічне пристрій. Набір з трьох функцій (НЕ, І, АБО) є базисом. Однак, базис (НЕ, І, АБО) не є мінімальним. З нього можна виключити одну з функцій І або АБО. Набори (НЕ, І), а також (НЕ, АБО) з двох функцій служать базисами. Дійсно функцію І можна реалізувати через функції (НЕ, АБО):
Функцію АБО можна реалізувати через функції (НЕ, І):
Обмежуючись базисами (НЕ, І); (НЕ, АБО) для виконання виключеною однієї операції потрібно проводити додатково три операції НЕ, що економічно недоцільно. Тому на практиці часто використовують немінімально базис трьох функцій (НЕ, І, АБО).
Досить зручно технічно реалізуються на мікросхемах логічні елементи, що поєднують в собі зазначені функції. Зручність пояснюється тим, що транзистор інвертує фазу вхідного сигналу, змінює її на 180 °. Це елементи І-НЕ (штрих Шеффера) і АБО-НЕ (стрілка Пірса).
Кожен з елементів (І-НЕ), (АБО-НЕ) окремо є функціонально повним базисом, дозволяє синтезувати будь-яке як завгодно складний пристрій. Розглянемо реалізацію функцій НЕ, І, АБО в базисі (АБО-НЕ):
Для інверсії необхідно подати вхідний сигнал на обидва входи. Для кон'юнкції - спочатку инвертировать вхідні сигнали, а потім застосувати операцію АБО-НЕ. Для диз'юнкції - провести операцію АБО-НЕ, після чого инвертировать отриманий результат:
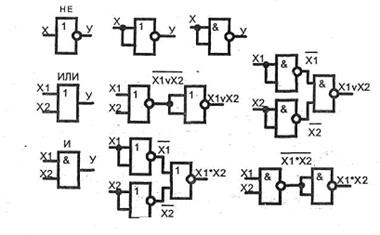
В базисі (І-НЕ) функції НЕ, І, АБО отримують сле-дмуть чином:
Легко помітити, що формули (24), (25) подібні. Їх схемне рішення показано на рис.
Привабливість базисів з однієї логічної функції (І-НЕ) або (АБО-НЕ) полягає в тому, що все логічне пристрій побудовано тільки на однотипних логічних елементах. Отримуємо логічну схему, яка володіє регулярною структурою. Необхідно тільки здійснити комутацію однакових логічних елементів. Базиси на логічних елементах (І-НЕ), (АБО-НЕ) широко використовуються при проектуванні пристроїв, зручні для реалізації в великих інтегральних схемах. Зменшення номенклатури до одного типу, таким чином, полегшує проектування пристроїв. Додаткові інвертори на входах покращують здатність навантаження і служать для формування сигналів лот. 1 і лог. 0 достатнього рівня.