Існують нескінченні множини, елементи яких не можна перенумерувати. Такі безлічі називаються незліченними.
Теорема Кантора. Безліч всіх точок відрізка [0, 1] незліченно.
Нехай безліч точок відрізка [0, 1] лічильно. Значить, ці точки можна перенумерувати, т. Е. Розташувати у вигляді послідовності x1. x2 ... xn. ....
Розіб'ємо відрізок [0, 1] на три рівні частини. Де б не знаходилася точка x1. вона не може належати всім відрізкам. . . Тому серед них є відрізок D1. який не містить точку x1 (рис. 1.7). Візьмемо цей відрізок D1 і розділимо його на три рівні частини. Серед них завжди є відрізок D2. який не містить точку x2. Розділимо цей відрізок на три рівні частини і т. Д. Отримаємо послідовність відрізків D1 É D2 É D3 É...ÉDn É.... В силу аксіоми Кантора сходиться до деякій точці x при n ® ¥. За побудовою ця точка x належить кожному відрізку D1. D2. D3, ..., Dn. ..., т. Е. Вона не може збігатися з жодною з точок x1. x2, ... xn. ..., т. Е. Послідовність x1. x2 ... xn. ... не вичерпує всіх точок відрізка [0, 1], що суперечить початковим припущенням. Теорема доведена.
Безліч, еквівалентну безлічі всіх точок відрізка [0, 1] називається безліччю потужності континууму.
Так як безлічі точок інтервалів, відрізків і всієї прямий еквівалентні між собою, то всі вони мають потужність континууму.
Щоб довести, що дане безліч має потужність континууму, досить вказати взаємно однозначна відповідність між даними безліччю і безліччю точок відрізка, інтервалу або всієї прямої.
З рис. 1.8 випливає, що безліч точок параболи y = x 2 еквівалентно безлічі точок прямої - ¥ 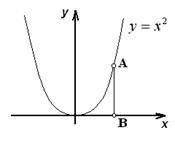
Встановити потужність континууму можна також, використовуючи наступні теореми про множини потужності континууму (наводяться без доказів).
Теорема 1. Безліч всіх підмножин рахункового безлічі лічильно.
Теорема 2. Безліч ірраціональних чисел має потужність континууму.
Теорема 3. Безліч всіх точок n- мірного простору при будь-якому n має потужність континууму.
Теорема 4. Безліч всіх комплексних чисел має потужність континууму.
Теорема 5. Множина всіх безперервних функцій, визначених на відрізку [a. b] має потужність континууму.
Отже, потужності нескінченних множин можуть відрізнятися. Потужність континууму більше, ніж потужність рахункового безлічі. Відповідь на питання, чи існують безлічі більш високої потужності, ніж потужність континууму, дає наступна теорема (наводиться без докази).
Теорема про множини вищої потужності. Безліч всіх підмножин даної множини має більш високу потужність, ніж дане безліч.
З цієї теореми випливає, що множин з максимально великою потужністю не існує.
Контрольні питання до теми 1
1. Нехай a Î А. Чи слід звідси, що a> А?
2. У якому випадку АА ÇВ?
3. Назвіть безліч, яке є підмножиною будь-якої множини.
4. Чи може бути безліч еквівалентно своєму подмножеству?
5. Потужність якого безлічі більше: безлічі натуральних чисел або безлічі точок відрізка [0, 1]?