Формулювання завдання: Близько окружності, радіус якої дорівнює R, описаний багатокутник, площа якого дорівнює S. Знайдіть його периметр.
Завдання входить до складу ЄДІ з математики базового рівня для 11 класу під номером 15 (Завдання з планіметрії).
Розглянемо, як вирішуються подібні завдання на прикладі і виведемо загальний спосіб вирішення.
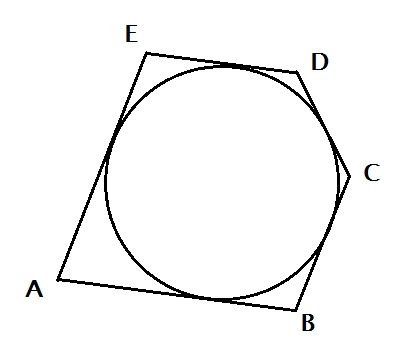
Близько окружності, радіус якої дорівнює 3, описаний багатокутник, площа якого дорівнює 33. Знайдіть його периметр.
Для вирішення даного завдання з'єднаємо центр окружності з усіма вершинами багатокутника і проведемо висоти в одержані трикутниках до сторін багатокутника.
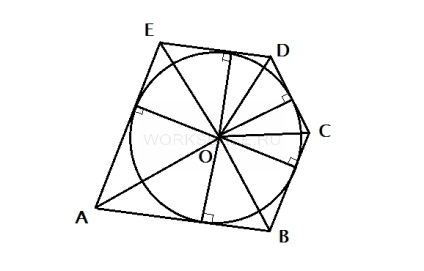
Щоб отримати площу багатокутника, отримаємо площі всіх 5 трикутників і складемо їх. При цьому зауважимо, що висота кожного трикутника дорівнює радіусу кола.
SABCDE = 1/2 ⋅ R ⋅ (AB + BC + CD + DE + EA)
Зауважимо, що в дужках вийшла сума довжин всіх сторін, тобто периметр P. Тому можна перетворити площу багатокутника в такий вигляд:
SABCDE = 1/2 ⋅ R ⋅ P
Залишилося підставити конкретні значення і висловити периметр:
P = 33/3 ⋅ 2 = 22
Таким чином, периметр багатокутника дорівнює 22.
У загальному вигляді рішення даної задачі з планіметрії виглядає наступним чином:
ПЕРИМЕТР багатокутника = 2 ⋅ S / R
де S - площа багатокутника, а R - радіус вписаного в нього кола.
Залишається лише підставити конкретні значення і підрахувати результат.