4. МОДЕЛІ Взаємодія ГАЗ - ТВЕРДОЕ ТІЛО
У цій частині посібника будуть розглянуті моделі, що лежать в основі опису процесів адсорбції - десорбції і перенесення енергії і імпульсу молекул в системі газ - тверде тіло.
4.1. Узагальнена модель взаємодії
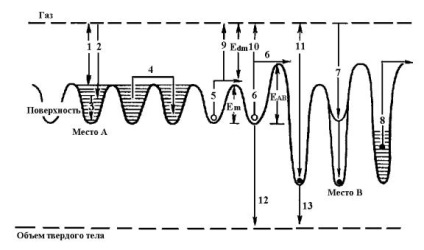
При зіткненні молекули газу з поверхнею твердого тіла відбуваються процеси, які можна представити у вигляді схеми, зображеної на рис. 4.1. Тут і далі ми будемо користуватися терміном «молекула», маючи на увазі при цьому всі частинки, що існують в газовій фазі, в тому числі і атоми [3].
Мал. 4.1. Схема процесів взаємодії частинок газу з твердим тілом
1. Молекула зазнає пружне розсіяння і повертає в газову фазу. Як і при пружному розсіянні електронів, цей процес може привести до ефектів дифракції.
2. Молекула передає твердого тіла частину своєї кінетичної енергії і виявляється утриманої центром слабкою адсорбції. Цей стан (А) відповідає самим дрібним потенційним ямах і називається фізичної адсорбцией. При цьому відбувається процес обміну енергією між твердим тілом
і вдаряються об нього молекулою і цей процес називають акомодацією.
3. Молекула спочатку утримується твердим тілом в стані А, зв'язок між молекулою і поверхнею колебательно збуджена, але при подальшому обміні енергією з твердим тілом молекула може виявитися на нижньому рівні потенційної ями.
4. Молекула може потрапити на нижній рівень потенційної ями А чи не при первинному зіткненні з поверхнею, як у випадку 3, а перестрибнувши на сусідній центр і втративши при цьому енергію збудження.
5. Молекула, що знаходиться на нижньому рівні потенційної ями А, може переміститися до сусіднього центру А, отримавши від кристалічної решітки
теплову енергію, достатню для подолання енергетичного бар'єра E m.
6. Якщо на поверхні є другий стан B з більш високою енергією зв'язку, відповідне хемосорбції, то молекула сусіднього центру А може переміститися в стан B, отримавши енергію активації E AB. У цьому випадку стан A є рухомим попередником стану B.
7. Стани А і B можуть розташовуватися практично в одній і тій же точці поверхні і молекула, потрапляючи в стан А з газової фази, може перейти прямо в стан B без переміщень по поверхні. Такий процес розглядався раніше (див. 2) при описі має місце в процесі взаємодії водню з металом переходу від фізичної адсорбції до слабкої хемосорбції. У цьому випадку стан А називають нерухомим попередником стану В.
8. При утворенні міцних хемосорбціонних зв'язків молекул адсорбата з поверхнею звільняється велика кількість енергії, яка, як і для описаної вище стадії 4, не поглинається повністю тим центром В, на якому сталася первісна хемосорбция. Тоді молекула буде дифундувати з одного стану Іншим до тих пір, поки не передасть кристалічній решітці достатню кількість енергії, щоб затриматися на певному центрі.
9. Молекула може десорбувати. В даному випадку має місце десорбція десорбція в ході дифузії (або міграції). При цьому молекулі
потрібна енергія активації E dm.
10. Десорбція зі стану А з енергією активації E dA. 11. Десорбція зі стану В з енергією активації E dB.
12. Переміщення молекули зі стану А в обсяг твердого тіла з утворенням тривимірного з'єднання з адсорбентом.
13. Те ж зі стану В.
На перераховані вище стадії можуть впливати взаємодії між адсорбованими частинками, які ми вважали незалежними один від одного.
Теоретичного опису всіх перерахованих стадій на даний момент немає. Однак є досить розвинені моделі первинного зіткнення молекули газу з поверхнею. Деякі з них будуть розглянуті нижче.
3.3. Розсіювання молекул поверхнею. коефіцієнти акомодації
Розглянемо кілька прикладів, пов'язаних з впливом взаємодії «газ - поверхня» на перебіг і теплообмін в розріджених газах. Згадаймо, що газ вважається розрідженим, якщо в ньому немає потрійних зіткнень молекул. Реально при звичайних температурах газ можна вважати таким аж до декількох десятків і навіть сотні атмосфер. Питання течії і теплообміну такого газу розглядаються «динамікою розрідженого газу». Найважливішою характеристикою системи в динаміці розрідженого газу є число Кнудсена Kn. яке визначається як відношення середньої довжини вільного пробігу молекул газу λ до характерного геометричного параметру завдання d. Розділ динаміки розрідженого газу, що стосується випадку великих розрідження (Kn = λ / d → ∞), називають «супераеродінамікой». Проблеми динаміки розрідженого газу (і супераеродінаміка особливо) тісно пов'язані з проблемою опису межфазовой кордону «газ - тверде тіло».
Перше якісне спостереження впливу взаємодії молекул з поверхнею при перебігу газів в каналах було проведено ще в минулому столітті. У 1875 р Кундт і Варбург помітили, що потік газів через трубу при дуже низькому тиску істотно вище, ніж передбачає формула Пуазейля (яка, як відомо, описує течія в'язкої рідини в каналі за умови рівності нулю швидкості на стінці). Вони визначили цей ефект, як «ковзання» на кордоні газ - тверде тіло. Максвелл в 1879 р припустив, що це ковзання могло бути результатом того, що є деяка частка молекул α τ. які падають на поверхню, приходять в
теплова рівновага з нею і випаровуються з поверхні дифузно, в той час, як частка молекул (1 - α τ) відбивається від поверхні дзеркально з перевернутої
нормальної складової імпульсу.
Більш детальний розгляд ситуації показує, що навіть у разі повністю дифузного віддзеркалення молекул від стінки профіль швидкості газу в каналі не відповідає рішенню рівняння Нав'є - Стокса. Тому для опису подібних явищ потрібно рішення рівняння Больцмана з заданими «істинними кінетичними» умовами на стінці [6].
Аналогічний ефект «температурного ковзання» виникає при наявності теплового потоку між газом і твердим тілом. Вперше цей ефект був описаний Смолуховським в 1898 р Для кількісної характеристики ефекту Кнудсен в 1910 р ввів поняття коефіцієнта акомодації. Згідно Кнудсеном, коефіцієнт акомодації є міра ефективності енергообміну на поверхні розділу між газом і твердим тілом, що знаходиться при різних температурах. Йому і Смолуховським належать перші вимірювання коефіцієнта акомодації.
Найбільш істотним є внесок взаємодії молекул з поверхнею в області сильно розрідженого газу (так званий, кнудсеновскій режим течії і теплообміну). Однак надійних експериментальних даних в цій області до недавнього часу не існувало. Стимулом до таких досліджень стало бурхливий розвиток космічної техніки, а також ультрависоковакуумной техніки і засобів діагностики поверхні.

Вплив взаємодії молекул з поверхнею на газодинамічну провідність каналів можна проілюструвати порівнянням експериментальних даних за течією газів через дуже короткий і дуже довгий канали (рис. 3.10; 3.11). У першому випадку частка молекул, що зіткнулися з бічною поверхнею каналу в загальному потоці газу, занадто мала. У другому випадку практично всі молекули, що виходять з каналу, несуть інформацію про взаємодію зі стінкою. Безрозмірна провідність M / M 0 визначалася як відношення експериментального потоку
до теоретичного, розрахованому для свободномолекулярного межі (по діаметру каналу). Теоретичне значення потоку в разі довгого каналу розраховувалося в припущенні повністю дифузного віддзеркалення молекул від стінки. З наведених прикладів видно, що наявність протяжної кордону вздовж потоку призводить до помітного вкладу взаємодії молекул з поверхнею в величину газодинамической провідності каналу. Цей внесок залежить від ступеня розрідженості газу (режиму течії) і природи молекул.
Мал. 3.10. Газодинамічна провідність короткого каналу (майже ідеального отвори). Відношення довжини каналу до діаметру 0,03

Мал. 3.11. Газодинамічна провідність довгого циліндричного скляного каналу. Відношення довжини каналу до діаметру 300
У табл. 3.2 наведені середні експериментальні значення провідності довгого скляного каналу по газам He. Ne і Ar в свободномолекулярном режимі (Kn → ∞). У цій же таблиці наведені
експериментальні похибки вимірювань Δ M.
Свободномолекулярная провідність довгого скляного каналу
- пуазейлевская провідність, що залежить від тиску P. B -
складова провідності, яка визначається «ковзанням», r - радіус каналу, "- його довжина, η - коефіцієнт в'язкості газу, k - постійна Больцмана, T -
температура, m - маса молекули газу, σ - константа ковзання (для моделі БГК, при повністю дифузному відображенні молекул σ T = 1,147).

На рис. 3.12 приведена експериментальна залежність константи ковзання від роду газу, отримана для довгих скляних циліндричних каналів. Для найпростішої схеми граничних умов в формі Максвелла величина σ може бути виражена через α τ наступним чином:
де γ залежить від числа Кнудсена в каналі і факторів взаємодії молекул газу з поверхнею каналу. γ приймає значення в інтервалі від 0 до ½.
Експериментальні дані для He і Ar представлені на рис. 3.13. Цей ефект вперше вивчався Кнудсеном на отворі і відомий як ефект термомолекулярная різниці тисків, або ефект Кнудсена.

Мал. 3.13. Експериментальна залежність γ для довгого каналу від ступеня
розрідженості газу і природи молекул (суцільна крива - теорія для повністю дифузного віддзеркалення молекул)
Експерименти показують, що ефект термомолекулярная різниці тисків в довгих каналах, як і в випадку отвори, найбільш істотний в області свободномолекулярного режиму по діаметру каналу, однак, на відміну від отвору, ефект в довгих каналах сильно залежить від газу. Ця обставина досить переконливо демонструє внесок розсіювання молекул поверхнею в процес неізотермічного течії газів.
Виключно важливу роль в техніці грають процеси теплообміну між газом і твердим тілом. При розрахунку різних теплообмінних пристроїв, теплового режиму літальних апаратів в кінцевому рахунку доводиться мати справу з ефективністю енергообміну між молекулами газу і поверхнею твердого тіла. Механізм тепловіддачі в газ від реальних поверхонь в загальному випадку є досить складним, проте з мікроскопічної точки зору головна проблема полягає в описі розсіювання молекул поверхнею в так званому шарі Кнудсена (тобто на відстані середнього вільного пробігу молекул від поверхні). Експериментального дослідження розсіювання молекул поверхнею твердого тіла присвячено чимало робіт. Однією з основних вимірюваних величин в цих роботах є коефіцієнт акомодації енергії [2].
Найпростішою системою, в якій можуть бути реалізовані вимірювання коефіцієнтів акомодації енергії, може служити система довгих коаксіальних циліндрів при різних температурах, між якими знаходиться газ при низькому тиску. Якщо зовнішній циліндр багато більше внутрішнього і режим теплообміну по газу свободномолекулярний, то величина теплового потоку між циліндрами (якщо знехтувати випромінюванням і перенесенням тепла через торці циліндрів) буде повністю визначатися ефективністю енергообміну між молекулами газу і поверхнею внутрішнього циліндра,

тобто коефіцієнтом акомодації енергії молекул α E. Питомий тепловий потік q M в цьому випадку може бути записаний у такий спосіб:
З наведеного прикладу видно, що залежність теплового потоку від взаємодії «газ - поверхня твердого тіла» може бути дуже істотною (тепловий потік прямо пропорційний фактору взаємодії
Мал. 3.14. Залежність наведеного теплового потоку q M від роду газу і числа Кнудсена
Взаємодія молекул з поверхнею призводить до виникнення температурного стрибка на кордоні «газ - тверде тіло» в континуальному режимі теплообміну. Наявність цього фактора доводиться враховувати, наприклад, при вимірюванні коефіцієнтів теплопровідності газів.
З теоретичної точки зору головна проблема в описі всіх вищезазначених явищ полягає в завданні граничних умов до рівняння Больцмана. Іншими словами, необхідно знати функцію розподілу відбитих від поверхні молекул f r і зв'язати її з функцією розподілу
падаючих молекул f i. Функція розподілу відбитих молекул записується в такий спосіб [6]:
де K (ξ i. ξ r)
відбитими молекулами, і E s - енергія, яку несли б відображені
молекули, якби газ був в рівновазі з поверхнею.
Для вимірювання коефіцієнтів акомодації можна використовувати вищенаведені експериментальні підходи, тобто обчислювати α τ і α E
безпосередньо з даних за течією і теплообміну розріджених газів. Однак в цьому випадку важко контролювати стан поверхні і неможливо судити про кутовому розподілі відображених молекул, що буває важливо знати при вирішенні деяких завдань.
Іншим експериментальним підходом, що дозволяє досліджувати кутову залежність в розподілі відображених молекул, є підхід, заснований на розсіянні молекулярного пучка. Застосування техніки молекулярних пучків забезпечує отримання індікатрісс розсіювання, інтегрування яких дає значення коефіцієнтів акомодації. На рис. 3.15 наведено характерний вид індікатрісс розсіювання, одержуваних за допомогою техніки молекулярних пучків.
Застосування техніки, заснованої на розсіянні молекулярного пучка, більш зручно для отримання α τ і α E на чистих і контрольованих
В даний час є досить експериментальних даних по α τ і α E. але лише деякі з них отримані при контрольованих умовах на
поверхні. Особливо мало даних за коефіцієнтами акомодації тангенціального імпульсу молекул з тепловими швидкостями на чистих поверхнях або поверхнях, частково покритих адсорбованими плівками відомого складу.
Значення коефіцієнта акомодації реальних систем може змінюватися в широких межах (в загальному випадку від 0 до 1). Для однієї і тієї ж системи «гелій - вольфрам» в різних умовах на поверхні були отримані значення α E від 0,018 до 0,4. Це, значить, що теплові потоки для
такої системи в свободномолекулярном режимі теплообміну можуть відрізнятися більш ніж в 20 разів в залежності від стану поверхні.
Нещодавно група дослідників під керівництвом Штейнхеля (1976 г.) представила дані по α τ. отримані в умовах добре контрольованої поверхні.
Мал. 3.15. Характерний вид індікатрісс розсіювання: