За спеціальною домовленістю з редколегією та редакцією журналу «Квант»
При вирішенні механічних завдань неоціненну допомогу може надати використання поняття центру мас системи матеріальних точок. Одні завдання просто неможливо вирішити, не вдаючись до цього поняття, рішення інших з його допомогою може стати набагато простіше і наочніше.
Перед тим як обговорювати конкретні завдання, нагадаємо основні властивості центру мас і проілюструємо їх прикладами.
Центром мас (центром інерції) системи матеріальних точок назвемо точку, що характеризує розподіл мас в системі, координати якої визначаються формулами
Тут mi - маси матеріальних точок, що утворюють систему, xi. yi. zi - координати цих точок. Читачі, знайомі з поняттям радіуса-вектора, віддадуть перевагу векторну запис:
Приклад 1. Знайдемо положення центру мас, найпростішої системи, що складається з двох точок, маси яких m1 і m2 і відстань між ними l (рис. 1).
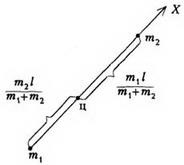
Направивши вісь X від першої точки до другої, отримаємо, що відстань від першої точки до центру мас (тобто координата центру мас) одно а відстань від центру мас до другої точки одно тобто відношення відстаней назад відношенню мас. Значить, в цьому випадку положення центру мас збігається з центром ваги.
1) Положення центру мас не зміниться, якщо якусь частину системи замінити однією точкою з масою, що дорівнює масі цієї підсистеми, і що знаходиться в її центрі мас.
Приклад 2. Розглянемо плоский однорідний трикутник і знайдемо положення його центру мас. Розділимо трикутник на тонкі смужки, паралельні одній зі сторін, і замінимо кожну смужку точкою, розташованої в її середині. Так як всі такі точки лежать на медіані трикутника, центр мас теж повинен лежати на медіані. Повторюючи міркування для кожної зі сторін, отримуємо, що центр мас знаходиться на перетині медіан.
2) Швидкість центру мас можна знайти, взявши похідну за часом від обох частин рівності (1):
де - імпульс системи, m - повна маса системи. Видно, що швидкість центру мас замкнутої системи постійна. Значить, якщо пов'язати з центром мас поступально рухається систему відліку, то вона буде інерційної.
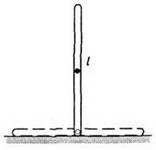
Приклад 3. Поставимо однорідний стрижень довжиною l вертикально на гладку поверхню (рис. 2) і відпустимо. У процесі падіння як горизонтальна складова його імпульсу, так і горизонтальна складова швидкості центру мас залишатимуться рівними нулю. Тому в момент падіння центр стрижня виявиться в тому місці, де спочатку стояв стрижень, а кінці стрижня змістяться по горизонталі на.
3) Прискорення центру мас одно похідною від його швидкості за часом:
де в правій частині рівності стоять тільки зовнішні сили, так як всі внутрішні сили скорочуються за третім законом Ньютона. Отримуємо, що центр мас, рухається так, як рухалася б уявна точка з масою, що дорівнює масі системи, під дією результуючої зовнішньої сили. Напевно, це саме фізична властивість центру мас.
Приклад 4. Якщо кинути палицю, привівши її у своїй в обертання, то центр мас палиці (її середина) буде рухатися з постійним прискоренням по параболі (рис. 3).
4) Нехай система точок знаходиться в однорідному полі тяжіння. Тоді сумарний момент сил ваги щодо будь-якої осі, що проходить через центр мас, дорівнює нулю. Це означає, що рівнодіюча сил тяжіння проходить через центр мас, тобто центр мас є також центром тяжіння.
5) Потенційна енергія системи точок в однорідному полі тяжіння обчислюється за формулою
де hц- висота центру мас системи.
Приклад 5. При викопуванні в однорідному фунті ями глибиною h і розкидання грунту по поверхні його потенційна енергія зростає на, де m - маса вилученого грунту.
6) І ще одна корисна властивість центру мас. Кінетична енергія системи точок може бути представлена у вигляді суми двох доданків: кінетичної енергії загального поступального руху системи, яка дорівнює, і кінетичної енергії Eотн руху щодо системи відліку, пов'язаної з центром мас:
Приклад 6. Кінетична енергія обруча, що котиться без проковзування по горизонтальній поверхні зі швидкістю υ, дорівнює
так як відносний рух в цьому випадку представляє собою чисте обертання, для якого лінійна швидкість точок обруча дорівнює υ (повна швидкість нижньої точки повинна дорівнювати нулю).
Тепер приступимо до розбору завдань на використання центру мас.
Завдання 1. Однорідний стрижень лежить на гладкій горизонтальній поверхні. До стрижня прикладають дві однакові за величиною, але протилежні по напрямку горизонтальні сили: одна сила прикладена до середини стрижня, інша - до його кінця (рис. 4). Щодо якої точки почне повертатися стрижень?
На перший погляд може здатися, що віссю обертання буде точка, що лежить посередині між точками докладання зусиль. Однак рівняння (3) показує, що оскільки сума зовнішніх сил дорівнює нулю, то дорівнює нулю і прискорення центру мас. Значить, центр стержня буде залишатися в спокої, тобто служити віссю обертання.
Завдання 2. Тонкий однорідний стрижень довжиною l і масою m привели в рух уздовж гладкій горизонтальній поверхні так, що він рухається поступально і одночасно обертається з кутовою швидкістю ω. Знайдіть, натяг стрижня в залежності від відстані x до його центру.
Перейдемо в інерційну систему відліку, пов'язану з центром стрижня. Розглянемо рух шматка стрижня, укладеного між розглянутої точкою стержня (розташованої на відстані x від центру) і його кінцем (рис. 5).
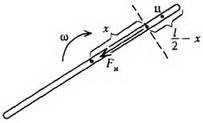
Єдиною зовнішньою силою для цього шматка є шукана сила натягу Fн. маса дорівнює, а його центр мас рухається по колу радіусом з прискоренням. Записуючи рівняння руху центру мас виділеного шматка, отримаємо
Завдання 3. Подвійна зірка складається з двох зірок-компонентів масами m1 і m2. відстань між якими не змінюється і залишається рівним L. Знайдіть період обертання подвійної зірки.
Розглянемо рух зірок-компонентів в інерціальній системі відліку, пов'язаної з центром мас подвійної зірки. У цій системі відліку зірки рухаються з однієї і тієї ж кутовою швидкістю по колу різних радіусів (рис. 6).
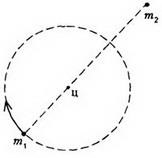
Радіус обертання зірки масою m1 дорівнює (див. Приклад 1), а її доцентровийприскорення створюється силою тяжіння до іншої зірки:
Бачимо, що період обертання подвійної зірки дорівнює
і визначається повною масою подвійної зірки, незалежно від того, як вона розподілена між зірками-компонентами.
Завдання 4. Дві точкові маси m і 2m пов'язані невагомою ниткою довжиною l і рухаються по гладкій горизонтальній площині. В деякий момент часу швидкість маси 2m дорівнює нулю, а швидкість маси m дорівнює υ і спрямована перпендикулярно нитки (рис. 7). Знайдіть натяг нитки і період обертання системи.
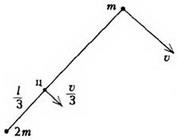
Центр мас системи знаходиться на відстані від маси 2m і рухається зі швидкістю. В системі відліку, пов'язаної з центром мас, точка масою 2m рухається по колу радіусом зі швидкістю. Значить, період обертання дорівнює (перевірте, що таку саму відповідь виходить, якщо розглянути точку масою m). Натяг нитки знайдемо з рівняння руху кожної із двох точок:
Завдання 5. На гладкій горизонтальній площині лежать два однакових бруска масою m кожен, пов'язаних легкої пружиною жорсткістю k (рис. 8). Першому бруска повідомляють швидкість υ0 в напрямку від другого бруска. Опишіть рух системи. Через якийсь час деформація пружини вперше досягне максимального значення?
Центр мас системи буде переміщатися з постійною швидкістю. В системі відліку центру мас початкова швидкість кожного бруска дорівнює, а жорсткість половинній пружини, яка з'єднує його з нерухомим центром мас, становить 2k (жорсткість пружини обернено пропорційна її довжині). Період таких коливань дорівнює
а амплітуда коливань кожного бруска, яку можна знайти із закону збереження енергії, становить
У перший раз деформація стане максимальною через чверть періоду, тобто через час .
Завдання 6. Куля масою m налітає зі швидкістю υ на спочивають куля масою 2m. Знайдіть швидкості обох куль після пружного центрального удару.
В системі відліку, пов'язаної з центром мас, повний імпульс двох куль дорівнює нулю як до, так і після coyдаренія. Легко здогадатися, яку відповідь для кінцевих швидкостей задовольняє одночасно і цій умові, і закону збереження енергії: швидкості залишаться такими ж, як до удару, по величині, але змінять свої напрямки на протилежні. Швидкість центру мас системи дорівнює. В системі центру мас першу кулю рухається зі швидкістю, а друга куля рухається назустріч першому зі швидкістю. Після удару кулі будуть розлітатися з такими ж швидкостями. Залишилося повернутися до первісної систему відліку. Застосовуючи закон складання швидкостей, знаходимо, що кінцева швидкість кулі масою m дорівнює і направлена назад, а швидкість покоїлося раніше кулі масою 2m дорівнює і направлена вперед.
Відзначимо, що в системі центру мас очевидним є твердження, що при ударі відносна швидкість куль не змінюється за величиною, але змінюється у напрямку. А так як різниця швидкостей при переході в іншу інерційну систему відліку не змінюється, можна вважати, що ми вивели цю важливу співвідношення і для початкової системи відліку:
де буква υ використовується для позначення початкових швидкостей, а u - для кінцевих. Це рівняння можна вирішувати спільно з законом збереження імпульсу замість закону збереження енергії (куди швидкості входять в другому ступені).
Завдання 7. Відомо, що при пружному нецентральному ударі двох однакових куль, один з яких до удару спочивав, кут розльоту дорівнює 90 °. Доведіть це твердження.
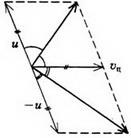
В системі центру мас нецентральних удар можна описати таким чином. До удару кулі зближуються з однаковими імпульсами, після удару вони розлітаються з такими ж за величиною, але протилежно спрямованими імпульсами, а пряма розльоту повертається на деякий кут відносно прямої зближення. Щоб перейти назад в початкову систему відліку, треба кожну кінцеву швидкість скласти (векторно!) Зі швидкістю центру мас. У разі однакових куль швидкість центру мас дорівнює, де υ - швидкість налітаючого кулі, і в системі відліку центру мас кулі зближуються і розлітаються з однаковими швидкостями. У тому, що після складання кожної кінцевої швидкості зі швидкістю центру мас виходять взаємно перпендикулярні вектори, можна переконатися з малюнка 9. А можна і просто перевірити, що скалярний добуток векторів і наближається до нуля в силу того, що модулі векторів дорівнюють один одному.
1. Стрижень масою m і довжиною l шарнірно закріплений за один з кінців. Стрижень відхилили на деякий кут від вертикального положення і відпустили. У момент проходження вертикального положення швидкість нижньої точки дорівнює υ. Знайдіть натяг в середній точці стержня в цей момент часу.
2. Стрижень масою m і довжиною l обертають в горизонтальній площині з кутовий швидкістю ω навколо одного з його кінців. Знайдіть залежність натягу стрижня від відстані x до осі обертання, якщо на іншому кінці закріплений маленький грузик масою М.
3. Знайдіть період коливань для системи, описаної в завданню 5 статті, але для брусків різних мас m1 і m2.
4. Виведіть відомі загальні формули для пружного центрального удару двох куль, використовуючи перехід в систему відліку центру мас.
5. Куля масою m1 налітає на спочивають куля меншою маси m2. Знайдіть максимально можливий кут відхилення налітаючого кулі при пружному нецентральному ударі.