Призма описана близько циліндра, якщо її заснування - багатокутники, описані навколо основ циліндра. Відповідно, циліндр вписаний в призму.
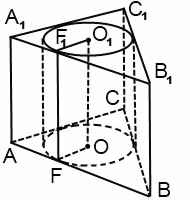
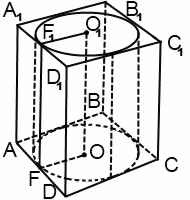
Циліндр можна вписати в призму, якщо в основу призми можна вписати коло. Радіус вписаного кола дорівнює радіусу циліндра. Висоти циліндра і призми рівні. У шкільному курсі вивчається тільки прямий круговий циліндр, відповідно, циліндр в цьому випадку вписаний в пряму призму.
Бічні грані описаного навколо циліндра призми є дотичними площинами до бічної поверхні циліндра.
Знайдемо відношення обсягу призми до обсягу вписаного в неї циліндра:
p - напівпериметр підстави призми, r - радіус вписаного в основу призми окружності і радіус циліндра, H - висота призми і висота циліндра.
Зокрема, відношення обсягу правильної трикутної призми до обсягу вписаного циліндра
Відношення обсягу правильної чотирикутної призми до обсягу вписаного циліндра
Для правильної шестикутної призми це відношення дорівнює
Відношення площі бічної поверхні призми до бічної поверхні вписаного циліндра:
Оскільки половина периметра підстави - напівпериметр,
Таким чином, якщо циліндр вписаний в призму, відношення площі бічної поверхні призми до бічної поверхні циліндра дорівнює відношенню обсягу призми до обсягу вписаного циліндра. Зокрема, відношення площі бічної поверхні правильної трикутної призми до площі бічної поверхні вписаного циліндра
Ставлення бічної поверхні правильної чотирикутної призми до бічної поверхні вписаного циліндра
Ставлення бічної поверхні правильної шестикутної призми до бічної поверхні вписаного циліндра
При вирішенні завдань, в яких циліндр вписаний в призму, можна вважати частину перетину комбінації тел площиною, що проходить через вісь циліндра. Для прямої призми це перетин - прямокутник, сторони якого рівні радіусу циліндра і висоті циліндра. Наприклад, AA1O1O: AA1 = H, AO = r.