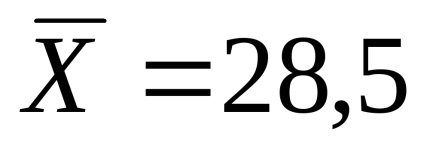Дані вимірювань показника "схильність до ризику"

Розрахуємо середні значення схильності до ризику в експериментальній (I) і контрольної (II) групах:

;

.

З отриманих розрахунків, видно, що вибіркова середня схильність до ризику в експериментальній групі азартних гравців (

) Вище, ніж та контрольній групі випадково відібраних людей ().

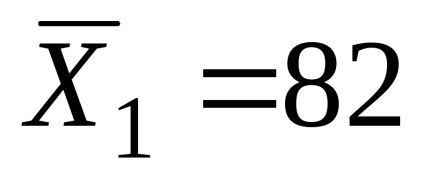
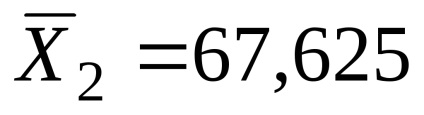
Чи можна стверджувати, що отримані відмінності статистично значущі, не випадкові?

Виберемо критерій для перевірки змістовної гіпотези про те, що у любителів азартних ігор схильність до ризику вище, ніж у групи випадковим чином відібраних людей.

Для перевірки подібної гіпотези - про рівність (відмінності) середніх значень (рівнів) ознаки в двох незалежних вибірках - пропонується кілька критеріїв [2], наприклад:

 параметричний критерій Стьюдента порівняння середніх;

 непараметрический критерій Розенбаума;

 непараметрический критерій Манна - Уїтні.

Так як, кожна з незалежних груп випробовуваних є вибіркою малого обсягу. причому

(), То для порівняння генеральних середніх в даному випадку найбільш коректним буде використання непараметричного критерію Манна - Уїтні.

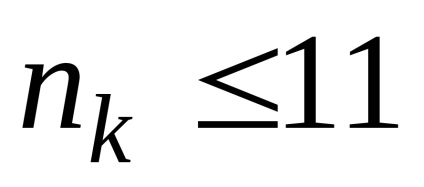
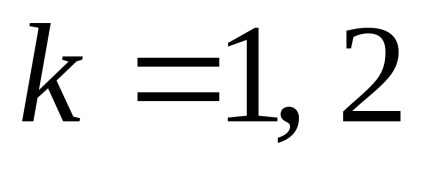
Сформулюємо статистичні гіпотези.

: Відмінність двох груп випробовуваних за рівнем схильності до ризику, є випадковим (формально: );

: Рівень показника "схильність до ризику" в експериментальній групі азартних гравців статистично значимо вище, ніж у контрольній групі випадково відібраних людей (формально: випадок спрямованих гіпотез).

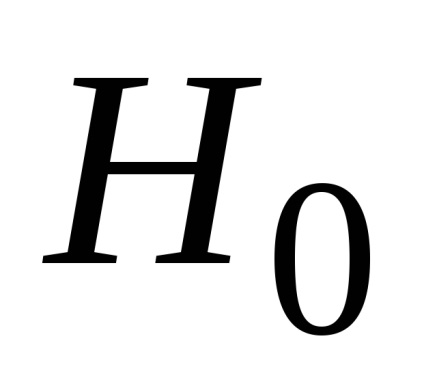
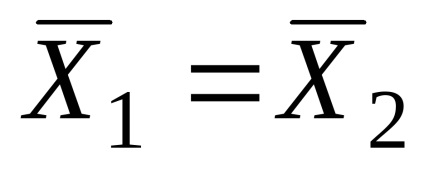
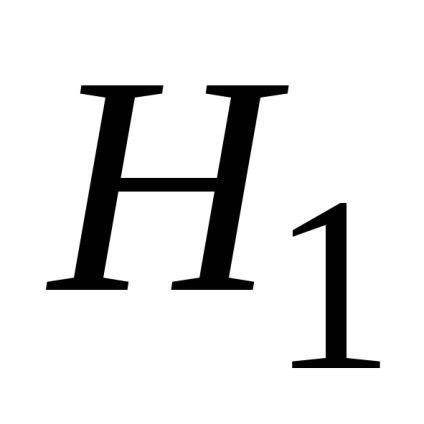
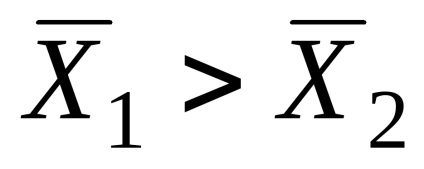
Для розрахунку емпіричного значення статистики

критерію Манна - Уітні необхідно проранжувати дані спостережень в двох групах випробовуваних як єдину вибірку.

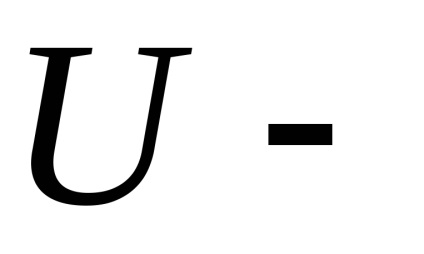
Процедура ранжирування здійснюється в два етапи:

впорядкування даних спостережень, наприклад, за зростанням;

власне ранжування, тобто приписування впорядкованим даними порядкових номерів (рангів).

Додатково, здійснюється перевірка правильності ранжирування: реальна сума отриманих рангів повинна збігатися з розрахункової теоретичної, що обчислюється за формулою

, деобсяг вибірки.

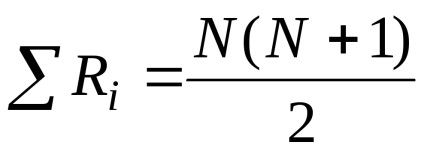
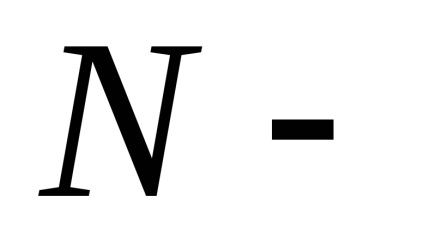
Для зручності ранжирування і обчислення рангових сум в кожній групі складемо розрахункову таблицю (див. Табл. 1.2).

Підрахунок рангових сум за експериментальною (I) і контрольної (II) вибірках

I. Експериментальна група

(

)

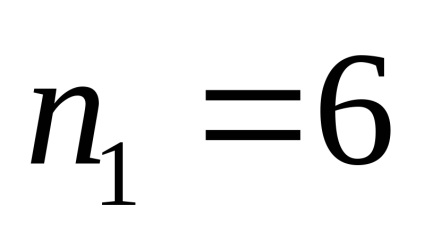
Перевірка правильності ранжирування:

реальна сума рангів;

теоретична сума рангів

().

Реальна сума рангів збігається з теоретичної, рівній 105, отже, ранжування проведено правильно.

Тепер можна обчислити емпіричне значення статистики

критерію Манна - Уітні за формулою,

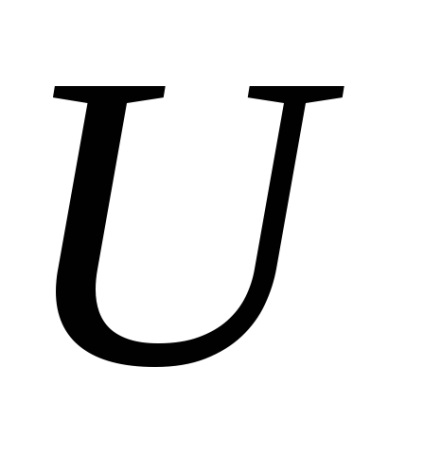
де більша з двох отриманих рангових сум;

обсяг вибірки з бóльшей сумою рангів .

.

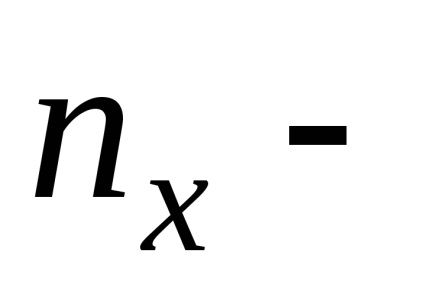
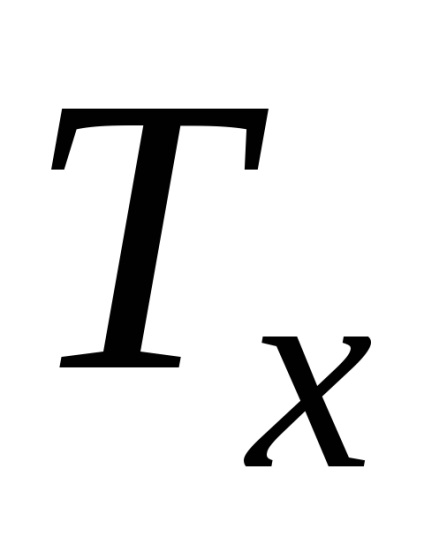
По таблиці критичних значень

критерію Манна - Уітні для перевірки спрямованих гіпотез [2, 3] визначимо:

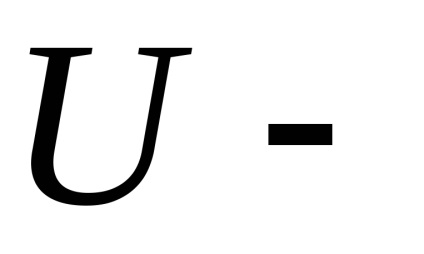
. отже, гіпотеза

() Про відсутність відмінностей у рівні досліджуваної ознаки двох незалежних вибірок проти спрямованої альтернативи() Про існування статистично значущих відмінностей в рівні ознаки може бути відкинута при.

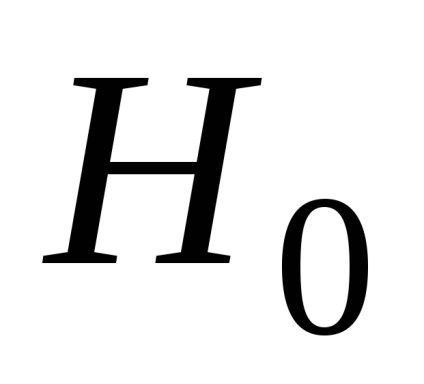
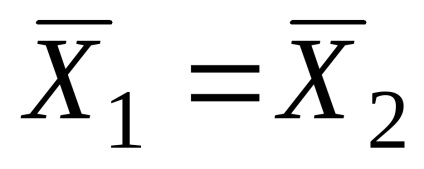
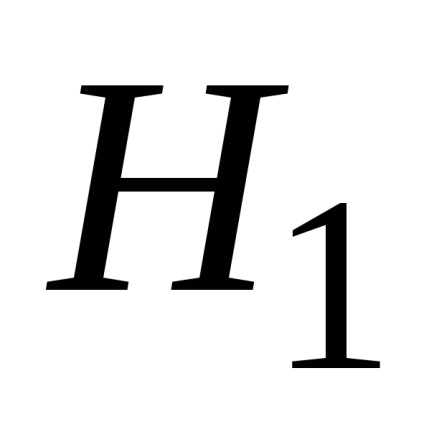
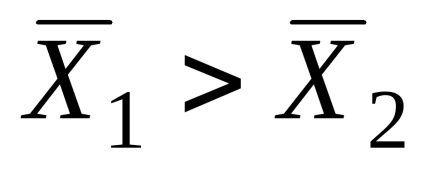
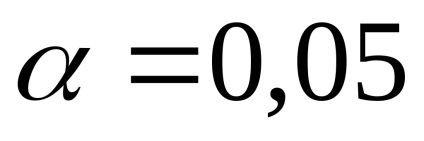
Таким чином, з упевненістю можна зробити висновок про те, що дані дослідження не суперечать гіпотезі

: В групі любителів азартних ігор значення показника, що відображає схильність до ризику, статистично значимо вище, ніж в групі випадковим чином відібраних людей.

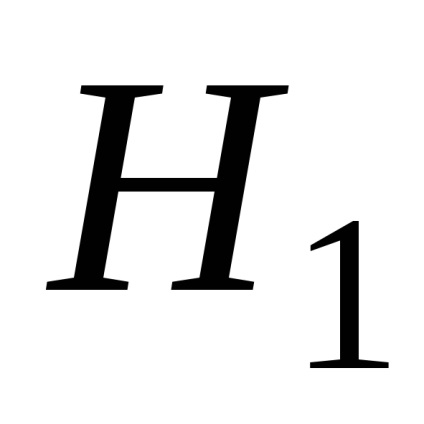
Приклад 2 - Визначення тісноти зв'язку (дослідження кореляції).

согласованность (кореляція) в групових ієрархіях відсутня;

согласованность (кореляція) в групових ієрархіях статистично значуща, не випадкова.

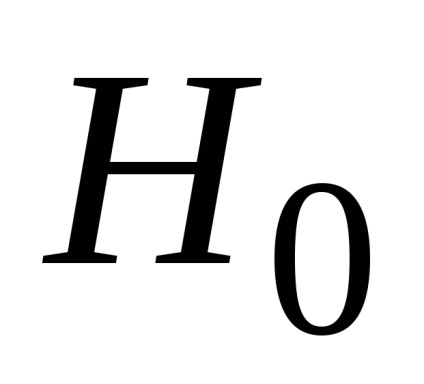
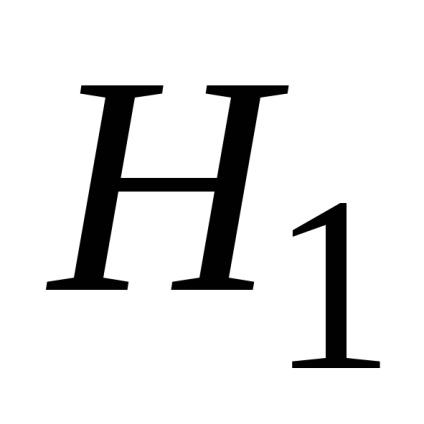
Для визначення факту існування узгодженості (зв'язку) і оцінки її тісноти між груповими ієрархіями (рангами) можна використовувати коефіцієнт рангової кореляції Спірмена

[1]:

.

Критичні значення коефіцієнта рангової кореляції Спірмена

в залежності від обсягу вибіркиі рівня значущостірівні [1, 3]:

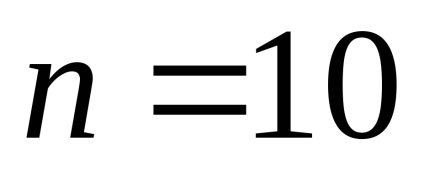
Приклад 3 - Перевірка статистичних гіпотез і дослідження кореляції.

 середній бал (оцінка) за результатами двох років навчання в університеті;

 знання основ програмування (тест: 21 питання на 30 хвилин);

Отримані дані наведені в таблиці 3.1.

Дослідника цікавлять питання:

Чи відповідають студенти МФ КемГУ відомої нормі тесту КОТ (IQ) для студентів університетів, що дорівнює 28 балів?

Яке співвідношення в рівнях виміряних показників у дівчат і юнаків?

Чи існує якийсь зв'язок між вимірюваними показниками?

1) Для відповіді наперво питання дослідження - Чи відповідають студенти МФ КемГУ нормі тесту КОТ (IQ) для студентів університетів, що дорівнює 28 балів? необходімо розрахувати вибіркове значення середнього уровняIQстудентов МФ КемГУ і вибрати відповідний статистичний критерій.

Середній рівень IQстудентов МФ КемГУ дорівнює

(Див. Табл. 3.2).

Схожі статті

• Визначити за допомогою тесту схильність до ризику