Кутова швидкість позначається грецькою буквою омега (w), вона говорить про те, на який кут повертається тіло за одиницю часу. Це величина дуги в градусній мірі, пройденої тілом за деякий час. Зауважте, якщо тверде тіло обертається, то кутова швидкість для будь-яких точок на цьому тілі буде величиною постійною. Ближче точка розташовується до центру обертання або далі - це не важливо, тобто від радіуса не залежить.
Одиницею виміру в цьому випадку буде або градус в секунду, або радіан в секунду. Часто слово «радіан» не пишуть, а пишуть просто з -1. Для прикладу знайдемо, чому дорівнює кутова швидкість Землі. Земля робить повний поворот на 360 ° за 24 год, і в цьому випадку можна говорити про те, що кутова швидкість дорівнює.
Також зверніть увагу на взаємозв'язок кутової швидкості і лінійної швидкості:
Необхідно відзначити, що рух по колу з постійною швидкістю - це окремий випадок руху. Однак рух по колу може бути і нерівномірним. Швидкість може змінюватися не тільки по напрямку і залишатися однаковою по модулю, але і змінюватися за своїм значенням, тобто крім зміни напрямку, існує ще і зміна модуля швидкості. В цьому випадку ми говоримо про так званому прискореному русі по колу.
Тема: Закони взаємодії і руху тіл
Урок 22. Рішення задач
Ерюткін Євген Сергійович
Урок присвячений вирішенню завдань
Завдання 1 присвячена закону всесвітнього тяжіння.
Умова: визначте висоту, на якій сила тяжіння буде в 3 рази меншою, ніж на поверхні Землі.
Дано: СІ Рішення:
h -. Відповідь: h »4685 км.
В умови вказано, що сила тяжіння повинна бути в 3 рази менше, ніж на поверхні Землі. Сила F1 - це сила тяжіння тіла до Землі на поверхні Землі, а сила F2 на деякій висоті.
Оскільки завдання відноситься до закону всесвітнього тяжіння. давайте цей закон запишемо, але зробимо це два рази. Перший раз - для тіла, яке знаходиться на поверхні Землі, а другий раз - для тіла, яке знаходиться на деякій висоті від поверхні Землі. Отже, F1 - це сила тяжіння, або сила тяжіння тіла, маса, якого m до самої Землі. Сам закон запишеться наступним чином:.
Запишемо тепер формулу для сили F2. яка відповідає силі взаємодії між малим тілом m і масою Землі, тілом маси Землі на деякій висоті h:.
З умови відомо, що F1 і F2 пов'язані залежністю:. Тепер об'єднуємо ці два рівняння в систему і ділимо рівняння один на одного.
Щоб зробити наступний крок, знадобиться витягти квадратний корінь з правої і з лівої частин.
Відповідь отримуємо у формулі, яка визначає висоту:.
Якщо тепер підставити всі відомі значення, то отримаємо відповідь: h »4685 км.
Це завдання добре показує можливість визначення висоти, на яку можна запустити супутник з таким розрахунком, щоб на нього діяла певного значення сила тяжіння. Це є важливою умовою при дослідженні руху супутників.
Завдання 2 присвячена криволинейному руху.
Умова: велосипедист рухається по заокругленню дороги, радіус заокруглення дороги 50 м, швидкість велосипедиста 36 км / год. Визначте доцентровийприскорення велосипедиста, що проходить закруглення дороги, і визначте силу тертя, яка діє на велосипед.
Дано: СІ Рішення:
Знайти потрібне АЦ і силу тертя, яка діє на велосипедиста. Для цього в першу чергу 36 км / год переведемо в систему СІ - 10 м / с. Звернемося до вирішення. Згадайте, що доцентровийприскорення визначається як відношення квадрата швидкості до радіуса заокруглення дороги:.
В цьому випадку можна записати.
Ось це і є доцентровийприскорення. Тепер можемо говорити, раз у нас є доцентровийприскорення, тобто діє сила, спрямована до центру кола, значить, діє на противагу інша сила - адже тіло рухається по колу постійного радіуса без прослизання і пробуксовки. Це сила тертя між колесами і дорогою. У цьому випадку обов'язково ми повинні відзначити, що FТР = Fц. За другим законом Ньютона FТР = Fц = m. АЦ. Отже, FТР = 60. 2 = 120 H. Відповідь; АЦ = 2 м / с 2 і FТР = 120 H.
Відзначимо, що якби сила тертя і доцентрова сила були нерівні, то ми б спостерігали або прослизання, або пробуксовування велосипеда з цього заокругленню, що порушило б його рівновагу.
Отже, переходимо до заключної, третьої задачі, яка буде присвячена прямолінійного руху.
Умова: визначте початкову швидкість тіла, яке, рухаючись вертикально вгору, через 2 с після початку руху досягло швидкості 5 м / с. Визначте висоту, на якій виявиться тіло, коли швидкість його стане дорівнює 5 м / с.
h -. Відповідь: h = 30 м.
Почнемо з початкової швидкості. Подивіться, ми запишемо спочатку повне рівняння швидкості. . Згадайте, що прискорення вільного падіння при вирішенні завдань ми приймаємо рівним. Тепер нам обов'язково потрібно система відліку.
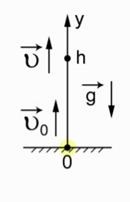
Мал. 1. Система відліку, вибрана для вирішення завдання
Система відліку пов'язана з поверхнею Землі. Тепер сумісний рівняння, рівняння швидкості до вибраної системи відліку. Зверніть увагу, щодо цієї системи відліку початкова швидкість спрямована вертикально вгору, збігається за напрямком з віссю у.
Швидкість через 2 с, яка визначена як 5 м / с, теж спрямована вертикально вгору -. Прискорення вільного падіння направлено вертикально вниз. Тут зазначеної стрілочкою ми позначили це прискорення. Далі записуємо рівняння: V = V0 - g. t. Підставляючи відомі значення, маємо: 5 = V0 - 10. 2.
Звідси отримуємо, що початкова швидкість, тобто швидкість, з якою тіло кинули вертикально вгору, буде дорівнює. Таким чином, використовуючи рівняння швидкості і систему відліку, ми визначили початкову швидкість. Наступний крок: визначення висоти.
Запишемо рівняння руху в загальному вигляді:.
Ми вже сказали, що початкова швидкість спрямована вертикально вгору, вона буде зі знаком плюс. Прискорення вільного падіння направлено щодо осі вниз і буде зі знаком мінус. В цьому випадку ми отримуємо висоту, довжину переміщення уздовж прямої - це. Відповідь виходить рівний h = 30 м.
Відповідь: h = 30 м.