Євразійський національний університет ім. Л.Н. Гумільова, м.Астана
декодування зі зворотним зв'язком
Згорткове кодування описується трьома цілими числами n, k і K. Від носіння називається ступенем кодування коду (інформація, прихо дящаяся, на закодований біт) і є мірою доданої з надлишкового. Ціле число K яв ляется параметром, який називається довжиною кодового обмеження.
Звичайний сверточних кодер, показаний на малюнку 1, реалізується з kK - розрядним регістром зсуву і п суматора за модулем 2, де K - довжина кодового обмеження [1].
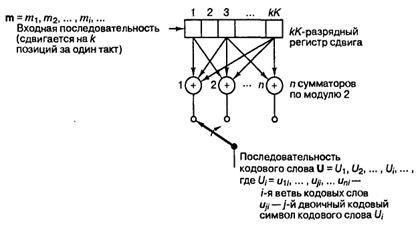
Малюнок 1 - сверточное кодер з довжиною кодового обмеження K і
ступенем кодування k / п
Довжина кодового обмеження - це кількість k -бітових зрушень, після яких один інформаційний біт може вплинути на вихідний сигнал кодера. У кожен момент часу на місце перших k розрядів регістра переміщаються k нових біт. Всі біти в регістрі зміщуються на k розрядів вправо, і вихідні дані п сумматоров послідовно дискретизируются. даючи, в результаті, біти коду. Потім ці симво ли коду використовуються модулятором для формування сигналів, які будуть передані по каналу. Так як для кожної вхідної групи з k біт повідомлення є п біт коду, ступінь кодування дорівнює, біт повідомлення на біт коду, де k<п.
Будемо розглядати часто використовувані виконавчі сверточ ні кодери, для яких k = 1, тобто ті кодують пристрої, в яких біти пові домлення зсуваються по одному біту за один раз [2, 3]. Для такого кодера за i - й момент часу біт повідомлення mi. буде переміщений на місце першого розряду регістра зсуву. Тоді всі попередні біти в регістрі будуть зміщені на один розряд вправо, а вихід ної сигнал n суматорів буде послідовно оцифрований і переданий. Так як для кожного біта повідомлення є n біт коду, то ступінь кодування буде дорівнює. У момент часу ti. маю щиеся n кодових символів складають i - e кодове слово гілки,. де - j - й кодовий символ, що належить i - му кодовим словом гілки. kK - розрядний регістр зсуву будемо називати K - розрядним регістром, а довжину кодового обмеження K - довжиною кодового обмеження в бітах.
Декодер зі зворотним зв'язком реалізує жорстку схему прийняття рішень щодо інформаційного біта в розряді j, виходячи при цьому з метрик, отриманих з разря-дов j, j + 1. j + m. де m - заздалегідь встановлений натуральне число. Ч ерез L позначимо дли-ну попередження, яка визначається як L = m + 1. L - це кількість прийнятих кодових символів, виражених через відповідне число вхідних бітів, задейст- Вова для декодування інформаційного біта. Рішення про те, чи є інформаційний біт 0 або 1, приймається в залежності від того, на якій гілці шлях мінімальної відстані Хеммінга переходить у вікні попередження з розряду j в розряд j + m. Пояснимо це на конкретному прикладі.
Розглянемо декодер зі зворотним зв'язком, призначений для згортальної коди зі ступенем кодування 1/2, який показаний на малюнку 2.
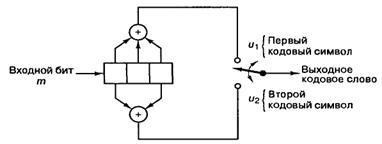
Малюнок 2 - сверточное кодер ступенем кодування 1/2 та
довжиною кодового обмеження K = 3
На малюнку 3 наведена дере-вовідная діаграма і робота декодера зі зворотним зв'язком при L = 3. Іншими словами, при декодуванні біта з гілки j декодер містить шляху з гілок j. j + 1 і j + 2.
Починаючи з першої гілки, декодер обчислює 2 L (вісім) сукупних метрик шляхів відстані Хеммінга і вирішує, що біт для першої гілки є нульовим, якщо шлях мінімальної відстані міститься у верхній частині дерева, і одиничним, якщо шлях мінімальної відстані знаходиться в нижній частини дерева. Нехай прийнята послідовність Z = 1 1 0 0 0 1 0 0 0 1. Розглянемо вісім шляхів від моменту t1. до моменту t3 в блоці A. (Рисунок 3). і розрахуємо метрики, срав- нівая ці вісім шляхів для перших шести прийнятих кодових символів (три гілки вглиб помножити на два символу для гілки). Починаючи з верхнього шляху і виписавши метрики Хеммінга загальних шляхів. видно, що вони мають таке значення:
метрики верхній частині 3, 3, 6, 4
метрики нижній частині 2, 2, 1, 3
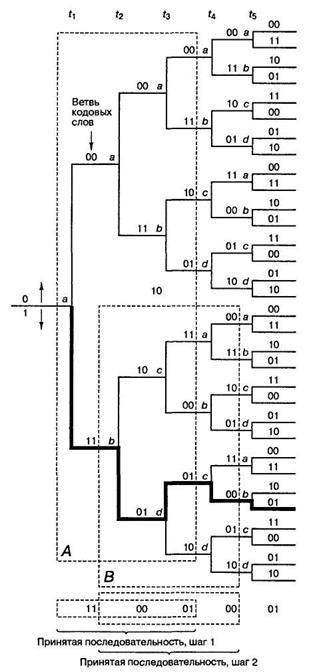
Малюнок 3 - Приклад декодування зі зворотним зв'язком
Найменша метрика міститься в нижній частині дерева. Отже, перший декодований біт є одиницею і визначається зрушенням вниз на дере- ве. Наступний крок буде полягати в розширенні нижньої частини дерева (виживає шлях) на один розряд глибше, і тут знову обчислюється вісім метрик, тепер уже для моментів t2 - t4. Отримавши, таким чином, два декодованих символу, тепер мо жно зрушити на два символу вправо і знову почати розрахунок метрик шляхів, але вже для шести кодових символів. Ця процедура видно в блоці В. І знову, простеживши метрики верхніх і нижніх шляхів, знаходимо таке:
метрики верхній частині 2, 4, 3, 3
метрики нижній частині 3, 1, 4, 4
Мінімальна метрика для очікуваної прийнятої послідовності знаходиться в нижній частині блоку В. Отже, другий декодіруемий біт також є одиницею.
Процедура триває до тих пір, поки не буде декодовано все повідомлення повністю. Декодер називається декодером зі зворотним зв'язком, тому що знайдене рішення назад подається в декодер, щоб потім використовувати його в оп- ределеніі підмножини кодових шляхів, які будуть розглядатися наступними. У двійковому симетричному каналі BSC декодер зі зворотним зв'язком може виявитися майже таким же ефек-ним, як і декодер, який працює за алгоритмом Вітербо. Крім того, він може виправляти всі найбільш ймовірні моделі помилки, які мають ваговий коефіцієнт менше або дорівнює. де df - просвіт коду. Важливим параметром розробки сверточного декодера зі зворотним зв'язком є довжина попередження L. Збільшення L призводить до підвищення ефективності кодування, але при цьому рас тет складність конструкції декодера.
2. Галлагер Р. Теорія інформації та надійний зв'язок. М. Радянське радіо, 1974, 720 с.
3. Fano R. M. Heuristic Discussion of Decoding. IRE Trans. Inf. Theory, vol. IT9. n. 2,1963, pp. 64 - 74.