
По суті для того, щоб розмити зображення необхідно якимось чином усереднити значення кольору кожного пікселя зображення з квітами його сусідів в межах деякого діапазону. Цей діапазон будемо називати радіусом розмиття. Очевидним рішенням буде наступне: скласти значення кольору для кожного пікселя, розташованого не далі, ніж радіус розмиття від поточного, по X і Y координаті, а потім поділити їх на квадрат двох радіусів розмиття плюс одиниця (так як ми зліва, справа, зверху і знизу вибираємо пікселі на відстані не більше ніж радіус + центральні пікселі). Однак давайте порахуємо, скільки ж пікселів нам доведеться отримати з зображення. Результатом роботи ось такого коду:
буде значення, рівне (1 + 2 • r) • (1 + 2 • r), де r - радіус розмиття. Для радіусу розмиття = 10 це виходить 441 вибірка! Це величезна складність, яку не скрізь можна використовувати. Саме для спрощення цієї складності і придумали двопрохідні алгоритми розмиття. Суть таких алгоритмів полягає в тому, що зображення розмивається спочатку по горизонталі (або по вертикалі) і зберігається у тимчасове зображення, після чого отримане зображення розмивається в іншому напрямку. В даному випадку ми отримаємо складність (1 + 2 • R) + (1 + 2 • R). Для радіусу розмиття = 10 ми отримуємо 42 вибірки на піксель, а це майже в R разів менше.
Також, при розмиття зображення слід враховувати ваги пікселів. При їх варіації можна отримати різний результат. Так, якщо всі пікселі будуть мати однакову вагу, ми отримаємо усереднене зображення. Якщо ж додати центральним пикселям більше ваги ніж крайнім, то ізобаженіе буде більш «сконцентровано». Для варіації ваг можна використовувати різні закони розподілу, відомих з математичної статистики.
Отже, розглянемо основні двопрохідні алгоритми розмиття. Для прикладу візьмемо ось таку вихідну картинку:

Усереднення сусідніх пікселів
Це найбільш простий алгоритм. Використовуємо рівномірний закон розподілу. В цьому випадку всі пікселі будуть мати однакову вагу. Покладемо радіус розмиття рівним десяти:
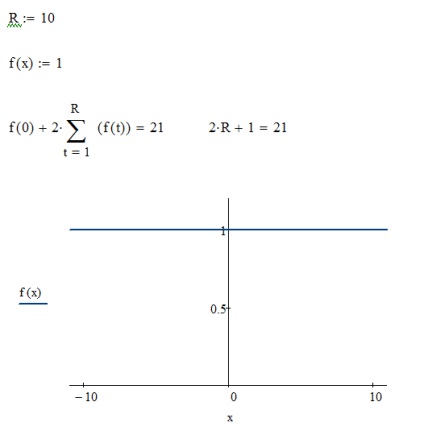
магічне число 21 є сумою всіх ваг сусідніх пікселів (звичайно ж для радіусу розмиття рівного 10). На це число нам потрібно буде поділити суму квітів сусідніх пікселів. Як видно, сума центрального і сусідніх пікселів (з кожної зі сторін) в точності дорівнює значенню 2 * R + 1. Таким чином немає необхідності вираховувати цю суму.
Розглянемо реалізацію даного алгоритму на шейдерний мовою GLSL
Вхідними параметрами є семплер для вихідного зображення і трикомпонентний вектор, який містить в собі крок розмиття і радіус. Кроком розмиття в даному випадку буде (1.0 / (ширина зображення); 0.0) для горизонтального розмиття і (0.0; 1.0 / (висота зображення)) для вертикального. У подальших реалізаціях будемо використовувати ту ж термінологію. Після двох проходів розмите зображення буде виглядати ось так:

Трикутний закон розподілу
Наступним за складністю алгоритмом є алгоритм, який використовує закон розподілу Сімпсона. В даному законі розподілу ваги сусідніх точок на текстурі, зі збільшенням відстані до центральної точки, зменшуються лінійно. Як і раніше, між іншим радіус розмиття рівним десяти. Так само як і раніше нам необхідно буде знайти суму всіх ваг сусідніх пікселів текстури і поділити фінальний результат на неї. Для цього, між іншим вага центрального піскелей рівним (r + 1). В такому випадку ваги сусідніх пікселів будуть змінюватися відповідно до функції f (x) (на зображенні нижче). Ваги крайніх точок в цьому випадку дорівнюватимуть одиниці.
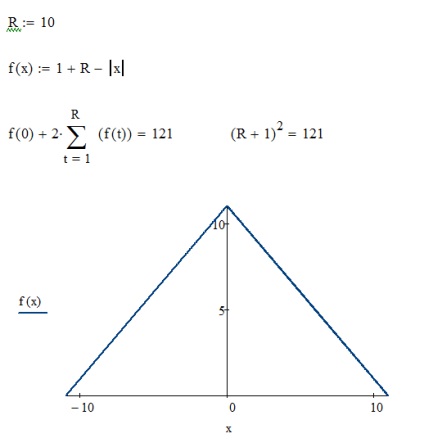
Сума ваг всіх пікселів в даному випадку буде виражатися формулою (R + 1) 2.
Реалізація даного алгоритму на GLSL приведена нижче:
Результат обробки зображення цим алгоритмом буде виглядати ось так:

Нормальний закон розподілу
Наступним алгоритмом розмиття, який ми розглянемо буде так зване розмиття по Гауса. Саме воно використовується в фотошопі. Суть його полягає в використанні нормального закону розподілу. Зазвичай нормальний закон розподілу включає в себе два параметри: математичне сподівання і дисперсію. Для нашого випадку будемо вважати математичне очікування рівним нулю. У цьому випадку закон розподілу включає тільки один параметр - дисперсію. Такий спрощений закон розподілу показаний на малюнку нижче (функція f (x)). Так як в даному законі використовується дисперсія величини, а не радіус, то скористаємося правилом трьох сигм. У ньому йдеться про те, що в діапазон -3 # 963 ;. + 3 # 963; потрапляє 99.73% всіх величин з розподілу. Покладемо радіус рівним десяти, в цьому випадку # 963; буде дорівнює 10/3 = 3 (дробову частина не враховуємо, так як ми робимо крок на ціле число пікселів в сторону від центрального).
Слід зауважити, що в даному алгоритмі сума ваг всіх сусідніх пікселів буде близька до одиниці. Тобто нам не доведеться ділити або множити отриманий результат на будь-яке число. Але також не слід забувати, що в обраний межа потрапляє не 100% величин, а тільки 99.73%. Це означає що сума буде менше одиниці і фінальне зображення буде затемнюватися. Щоб усунути цей недолік збільшимо змінимо вага центральної точки на (1.0 - [сума ваг сусідніх]) і в підсумку отримаємо суму ваг усіх пікселів дорівнює одиниці.
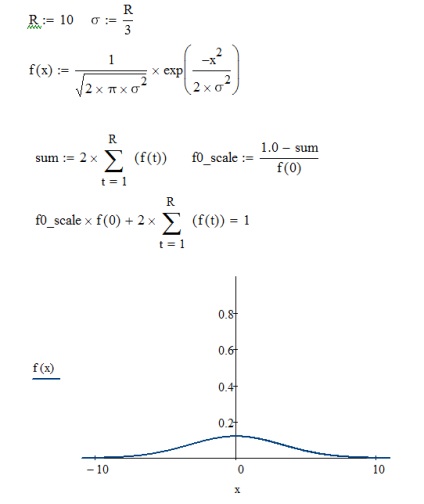
Розглянемо код даного алгоритму на GLSL:
Як бачимо, тут виконується дуже багато зайвих інструкцій. Кожен раз перераховуються константи і т.д. Давайте трохи оптимізуємо цей код:
1) винесемо сигма з під кореня і обчислимо константу 1.0 / sqrt (2.0 * PI),
2) так як сигма у нас не змінюється, отже не змінюється все вираз перед експонентою, а так же множник при x в вираженні всередині експоненти, отже все це можна порахувати один раз і винести «за дужки»,
3) позбудемося зайвої операції ділення на три, підставивши трійку в вирази.
Після виконаних операцій отримаємо ось такий ось шейдер
Такий оптимізацією ми не тільки зменшили розмір шейдера, а й збільшили швидкість приблизно о 1.15 рази (тестувалося при радіусі розмиття = 50). Це, погодьтеся, трохи, але корисно :)
Результат розмиття по Гауса буде виглядати наступним чином:

Покладемо радіус розмиття рівним 30 і порівняємо результат з розмиванням в фотошопі:


Перше зображення, розмите з радіусом 30 пікселів, друге - різниця між наведеними алгоритмом і фільтром фотошопа