При коченні еластичного (деформованого) колеса під дією силових факторів відбувається тангенціальна деформація шини, при якій дійсне відстань від осі обертання колеса до опорної поверхні зменшується. Це відстань називають динамічним радіусомrд колеса. Його величина залежить від ряду конструктивних і експлуатаційних факторів, таких, наприклад, як жорсткість шини і внутрішній тиск в ній, вага автомобіля, що припадає на колесо, швидкість руху, прискорення, опір коченню і ін.
Динамічний радіус зменшується зі збільшенням крутного моменту і зі зменшенням тиску повітря в шині. Величина rд дещо зростає зі збільшенням швидкості руху автомобіля внаслідок зростання відцентрових сил. Динамічний радіус колеса є плечем додатки штовхає сили. Тому його називають ещесіловим радіусом.
Кочення еластичного колеса по твердій опорній поверхні (наприклад, по асфальтовому або бетонному шосе) супроводжується деяким прослизанням елементів протектора колеса в зоні його контакту з дорогою. Це пояснюється різницею довжин ділянок колеса і дороги, що вступають в контакт. Це явище називають пружним проскальзиваніем шини, на відміну отскольженія (буксування), коли всі елементи протектора зміщуються щодо опорної поверхні. Пружного прослизання не було б за умови абсолютної рівності цих ділянок. Але це можливо лише в тому випадку, коли колесо і дорога мають контакт по дузі. Насправді ж, опорний контур деформованого колеса вступає в контакт з плоскою поверхнею недеформованою дороги, і прослизання стає неминучим.
Для обліку цього явища в розрахунках використовують поняття кінематичного радіуса колеса (радіуса кочення) rк. Таким чином, розрахунковий радіус каченіяrк є такий радіус фіктівногонедеформірованного колеса, яке при відсутності прослизання має з реальним (деформованим) колесом однакові лінійні (поступальні) швидкості каченіяv і кутового вращеніяωк. Тобто велічінаrк характерізуетусловний радіус, який служить для вираження розрахункової кінематичної залежності між швидкістю двіженіяv автомобіля і кутовий швидкістю обертання колесаωк:
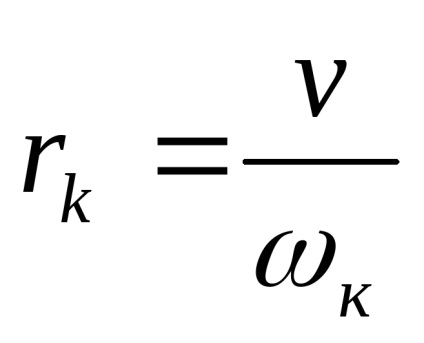
Особливістю радіуса кочення колеса є те, що він не може бути виміряна безпосередньо, а визначено лише теоретично. Якщо переписати наведену вище формулу як:
то з отриманого виразу видно, що визначити величину rк можна розрахунком. Для цього необхідно заміряти путьS. прохідний колесом заn оборотів, і розділити його на кут повороту колеса (φк = 2πn).
Величина пружного прослизання зростає при одночасному збільшенні еластичності (піддатливості) шини і жорсткості дороги або, навпаки, при збільшенні жорсткості шини і м'якості дороги. На м'якій грунтовій дорозі підвищений тиск в шині збільшує втрати на деформацію грунту. Зниження внутрішнього тиску в шині дозволяє на м'яких грунтах зменшити переміщення частинок грунту і деформації її шарів, що обумовлює зниження опору коченню і підвищення прохідності.
Однак, на твердій опорній поверхні при малому тиску відбувається надмірний прогин шин зі збільшенням плеча тертя кочення а. Компромісним рішення даної проблеми є використання шин з регульованим внутрішнім тиском.
У практичних розрахунках радіус кочення колеса оцінюється за наближеною формулою:
Для доріг з твердим покриттям (рух колеса з мінімальним прослизанням) приймають: rк = rd.