2. Постановка завдання
6. Побудова загального рішення матричним методом
7. Завдання Коші для матричного методу
Розглянемо систему лінійних рівнянь першого порядку, записану в нормальній формі:
де коефіцієнти аij. i = 1,2, .... n, к = 1,2, ..., n, є постійними величинами;
yi = yi (t), i = 1,2, ..., n - невідомі функції змінної t.
Якщо все bi (t) (i = 1,2, ..., n) покласти рівним нулю (bi (t) = 0), то вийде однорідна система, відповідна неоднорідною системі (1).
Позначаючи матрицю системи через А (х), а вектор
тоді систему (1) можемо переписати в матричній формі
, то отримуємо відповідну систему однорідних рівнянь
Будь-яка сукупність n функцій
визначених і безперервно диференційовних в інтервалі (a; b), називається рішенням системи (1) в цьому інтервалі, якщо вона звертає всі рівняння системи (1) в тотожності:
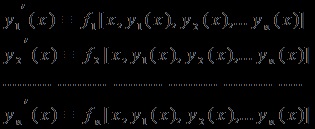
справедливі при всіх значеннях x з інтервалу (a, b). Загальне рішення неоднорідної системи являє собою суму загального рішення відповідної однорідної системи і приватного рішення неоднорідної.
2. Постановка завдання
Мета роботи: дослідження методів розв'язання системи диференціальних рівнянь з постійною матрицею:
;
;
1. Знайти власні числа і побудувати фундаментальну систему рішень (ФСР).
2. Побудувати фундаментальну матрицю методом Ейлера.
3. Знайти наближене рішення у вигляді матричного ряду.
4. Побудувати загальне рішення матричним методом. Дослідити залежність Жорданова форми матриці А від її власних чисел.
5. Вирішити задачу Коші.
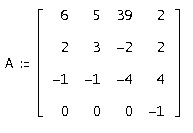
Вектор початкових умов: [1, 2, 3, 4]
Однорідної лінійної системою диференціальних рівнянь називається система рівнянь виду:
Якщо в матриці системи
= Const, то дана система називається системою з постійними коефіцієнтами або з постійною матрицею.
Фундаментальною системою рішень однорідної лінійної системи рівнянь називається базис лінійного простору рішень a, тобто n лінійно незалежних рішень цієї системи.
Для побудови фундаментальної системи рішень диференціального рівняння необхідно знайти власні числа характеристичного полінома, так як в залежності від їх виду (характеристичні числа можуть бути дійсними різними, кратними, комплексними) будується фундаментальна система рішень.
Для того щоб ця система n лінійних однорідних рівнянь з n невідомими мала нетривіальне рішення, необхідно і достатньо, щоб визначник системи (вронскиан) дорівнював нулю:
З цього рівняння ступеня n визначається значення k, при яких система має нетривіальні рішення. Рівняння (4) називається характеристичним.
Запишемо характеристичний поліном, для цього скористаємося функцією CHARPOLY
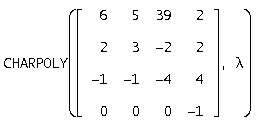
Для знаходження власних чисел скористаємося функцією SOLVE (U, l), яка повертає характеристичні числа матриці А в вектор l. отримаємо:
Вийшло два дійсно кореня
і два комплексно-сполучених кореня
. Отже, вектора, що утворюють фундаментальну матрицю, для даного типу коренів будуть перебувати окремо для
. Запишемо ФСР для даних для отриманих характеристичних чисел:
Матрицю y (x), стовпцями якої є рішення, що утворюють фундаментальну систему, називають фундаментальною матрицею.
І загальне рішення системи буде виглядати наступним чином:
Знайдемо рішення даної системи за допомогою методу Ейлера.
Метод Ейлера полягає в наступному.
Рішення системи (1) знаходиться у вигляді:
Функція (5) є рішенням системи (1), якщо
- власне значення матриці А, а а - власний вектор цієї матриці, що відповідає числу
. Якщо власні значення
n матриці А попарно різні і a1. a2. ..., an відповідні власні вектори цієї матриці, то загальне рішення системи рівнянь (1) визначається формулою:
Для випадку кратних коренів рішення системи приймає вигляд
де Pi (x) -поліноми ступеня не вище, ніж (к-1), що мають в сукупності до довільних коефіцієнтів. Так що серед коефіцієнтів цих поліномів до коефіцієнтів є довільними, а що залишилися до · n-k виражаються через них. Для відшукання коефіцієнтів поліномів підставимо рішення (6) у вихідну систему рівнянь, прирівняємо коефіцієнти при однакових функціях. Вирішимо систему по відношенню до (k · n-k) коефіцієнтів. Отримаємо вираз всіх коефіцієнтів через вільні.
Якщо для кратного власного значення
матриці А є стільки лінійно незалежних власних векторів
, яка його кратність, то йому відповідає k незалежних рішень вихідної системи:
Якщо для власного значення
кратності k є тільки m (m , можна шукати у вигляді добутку векторного багаточлена ступеня k - m на Щоб знайти вектори , треба підставити вираз (4) в систему (3). Прирівнявши коефіцієнти подібних членів в лівій і правій частинах системи, отримаємо рівняння для знаходження векторів . Для даного завдання були знайдені такі власні значення: . Побудували фундаментальну систему рішень: Знайдемо 1 рядок фундаментальної матриці рішень для характеристичного числа . Запишемо третій рядок рішень в загальному вигляді:
Де аij знайдемо з виразу:
Експонентою e A матриці А називається сума ряду
де Е - одинична матриця.
Властивість матричної експоненти:
а) якщо АВ = ВА, то е А + В = е А * е В = е В * е А;
б) якщо А = S - 1 * B * S, то е А = S -1 * e B * S, де матриця S - це матриця перетворення змінних із власного базису в базис вихідних змінних.
в) матриця y (t) = e At є рішенням матричної задачі Коші:
тобто є фундаментальною матрицею системи (1).
З властивості в) слід, що рішення y (t) системи (1) задовольняє умові y (0) = y0. визначається виразом y (t) = e At * y0. Таким чином, завдання знаходження рішень системи рівнянь (1) еквівалентна задачі відшукання матриці e At по матриці А.
Для обчислення матриці e At зручно представити матрицю А у вигляді:
,
де матриця S - це матриця перетворення змінних із власного базису в базис вихідних змінних, а BА - жорданова форма матриці А, тому що e At = S -1 * e Bt * S.
Жорданова форма матриці залежить від виду характеристичних чисел.
1. Нехай характеристичні числа дійсні кратні, тоді Жорданова форма матриці розмірності nxn має вигляд:
- дійсний корінь кратності n.
2. Якщо серед коренів характеристичного полінома є, як дійсні різні, так і дійсні кратні коріння, то матриця В має вигляд:
- дійсні різні корені, а
- дійсний корінь кратності 2.
3. При наявності серед коренів характеристичного полінома коренів комплексно-сполучених Жорданова клітина виглядає наступним чином:
комплексно пов'язаний корінь характеристичного полінома.
Так як в нашому випадку серед характеристичних чисел присутні, як комплексно-зв'язані коріння л = 2 - # 59329; ∨ л = 2 + # 59329 ;, так і дійсний різне коріння л = -1 ∨ л = 1, то жорданова матриця виглядає наступним чином:
З рівняння A * S = S * В, де S - невироджена матриця, отримуємо систему 16-го порядку, з якої знаходимо елементи матриці S. Отримана матриця S буде виглядати наступним чином:
Вирішуємо систему 16-го порядку з рівняння A * S = S * У

Доопределять деякі елементи і отримуємо наступну матрицю S:
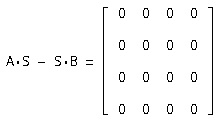
Значить матриця переходу знайдена вірно.
Для знаходження вектора рішень y необхідно помножити матрицю S на
- це вектор, елементи якого залежать від коренів характеристичного многочлена:
Для комплексних чисел
має наступний вигляд:
Для випадку коренів дійсних різних:
=
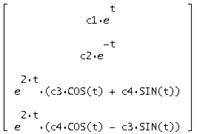
Звідси знайдемо спільне рішення у = S *
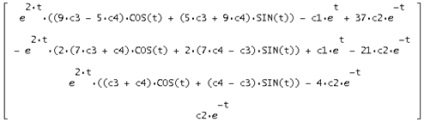
При підстановці рішення у вихідну систему виходить правильне рівність, з цього випливає, що рішення знайдено вірно:
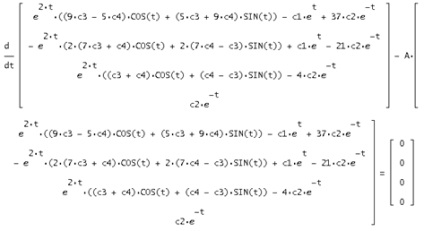
7. Завдання Коші для матричного методу
Необхідно з усіх рішень системи рівнянь знайти таке рішення, в якому y (i) (t) приймає задане числове значення y0i в заданій точці, тобто знайти значення сi для наступних заданих значень: x = 0, y = [1, 2, 3,4].
В вектор рішень y (t) підставляємо задані умови і вирішуємо отриману систему відносно c1, c2, c3, c4:
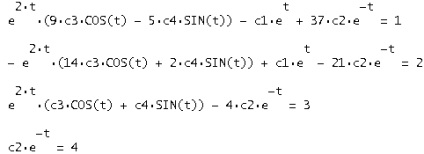
В результаті отримуємо:
При підстановці c1, c2, c3, c4в спільне рішення отримаємо рішення у формі Коші:
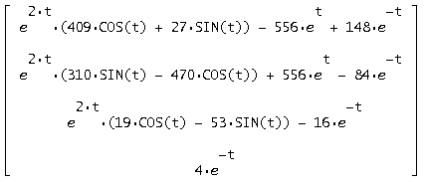
:

Вийшов нульовий вектор
. Отже, знайдена матриця є рішенням вихідної системи.
Нехай J - жорданова клітина матриці А. Для випадку дійсних різних коренів жорданова клітина буде виглядати наступним чином:
Нехай серед дійсних власних чисел матриці А є кратні. Жорданова клітина буде перебувати за такою формулою:
Наприклад, якщо кратність k = 2, то жорданову клітку матриці ми можемо записати так:
Якщо кратність k = 3, то жорданову клітку матриці ми можемо записати так:
Якщо ж серед трьох власних чисел
є корінням кратності 2, то жорданова форма буде виглядати наступним чином:
Якщо два власних числа матриці А є комплексними сполученими, то запис жорданової клітини буде виглядати так:
- уявна частина власного числа
.
Загальне рішення неоднорідної системи можна знайти за формулою: