Розглянемо систему m лінійних рівнянь c n невідомими (1). Для неї
Так як ранг матриці дорівнює максимальному числу її лінійно
незалежних рядків (по теоремі про ранзі матриці), то, можна зробити наступний висновок.
Якщо рядки розширеній матриці. а значить і рівняння системи (1), лінійно незалежні, то ранг r матриці дорівнює числу її рівнянь: r = m. якщо лінійно залежні, то r Наступні теореми дають відповіді на два важливих питання: 1) В якому випадку система (1) сумісна? 2) Якщо система (1) сумісна, то скільки рішень вона матиме? Теорема Кронекера-Капеллі. Система лінійних рівнянь сумісна тоді і тільки тоді, коли ранг основної матриці системи дорівнює рангу розширеної матриці цієї системи. Для спільної системи число r = r (А) = r () називається рангом системи. Теорема про кількість рішень. Нехай ранг спільної системи лінійних рівнянь дорівнює r. а число невідомих в системі дорівнює n. Якщо r = n. то система має єдине рішення; якщо r Результати дослідження системи (1) можна представити у вигляді схеми (рис. 2). Мал. 2 Дослідження систем лінійних рівнянь нехай r Рішення системи (1), в якому все n - r неосновних змінних дорівнюють нулю, називається базисним.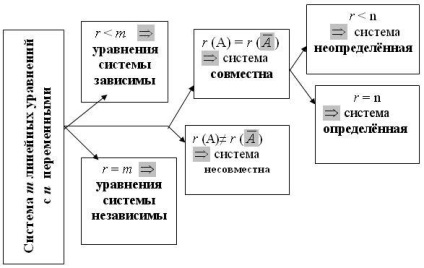
Схожі статті