Будь-яка система автоматичного регулювання може бути досить складною і складатися з цілого ряду елементів, з'єднаних між собою різними зв'язками. Об'єкт регулювання може складатися із з'єднання декількох об'єктів, а регулятор може мати інші елементи, крім основних, розглянутих раніше. Тоді структурна схема системи регулювання може мати вигляд
Зв'язки в системі можуть бути: основними, додатковими, додатковими зворотними.
Основна зв'язок - утворюється основний ланцюгом дії (основне проходження системи). Наприклад: mоб - 1 - 2 - 3 - # 966; - для об'єкта; # 966; → 4 - 5 - 6 - 7 - mрег - для регулятора.
Додаткова зв'язок - утворює шлях передачі впливів в доповнення до основної. Наприклад: елемент 9, включений паралельно елементу 6.
Додаткова зворотний зв'язок - спрямована з виходу якого-небудь елемента на його вхід або на вхід попередніх елементів. Наприклад: елемент 8 з подачею сигналу з виходу елемента 7 на вхід елемента 5.
Елементи, що входять в систему регулювання, повинні бути найпростішими, тобто пропускати сигнал від входу до виходу і поведінку його в часі має описуватися диференціальним рівнянням не вище другого порядку, яке завжди можна скласти, розглянувши фізику процесу.
Так як диференціальне рівняння складної системи регулювання скласти практично неможливого, в автоматиці використовується наступний підхід:
1) розбивають систему на найпростіші елементи;
2) отримують диференціальні рівняння елементів;
3) по диференціальнимирівняннями отримують їх передавальні функції;
4) розглядаючи сполуки елементів в системі регулювання, отримують передавальну функцію системи по передавальним функціям елементів;
5) з передавальної функції системи отримують диференціальне рівняння системи.
Складемо диференціальне рівняння бака з водою як об'єкта регулювання рівня води. Це елемент системи регулювання (рис.13):
Мал. 13. Q1. м 3 / с - приплив води; Q2. м 3 / с - витрата води з бака; S - перетин бака, = const, м2; Н0 - значення рівня в статичному режимі; DН = Н - Н0 - відхилення рівня від статичного (заданого) значення; V0 - об'єм рідини в баку в статичному режимі; DV - зміна обсягу рідини в динамічному режимі.
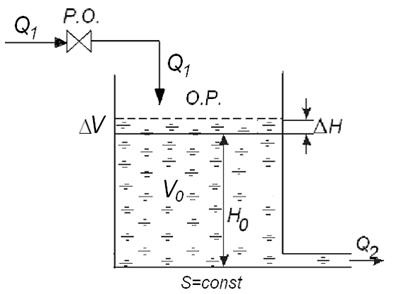
- рівняння балансу витрат в динаміці
Уявімо витрати в відхиленнях:
(З рівняння статичного режиму).
З малюнка слід, що рівень Н не впливає на приплив Q1. отже .Рівень H впливає на витрату води з бака Q2. отже, Q2 є функцією рівня. У теорії систем автоматичного регулювання розглядаються малі відхилення параметра (рівня Н) від заданого значення (Н 0). В цьому випадку можна прийняти, що вихідні величини змінюються пропорційно зміні вхідних величин. Виходячи з цього можна записати
де k н - коефіцієнт пропорційності (коефіцієнт посилення).
Тоді рівняння динаміки бака набирає вигляду
Запишемо рівняння (6.1) у вигляді
Введемо позначення:; і запишемо рівняння (6.2), використовуючи ці позначення
У цьому рівнянні До називають розмірним коефіцієнтом посилення. Він має розмірність відносини вихідної величини (DН) до розмірності вхідної величини (DQ1). Коефіцієнт при похідній Т [з] має розмірність часу і називається постійної часу. Це лінійне диференціальне рівняння.
При складанні диференціального рівняння будь-якого іншого елемента системи регулювання, в якому протікають інші фізичні процеси (наприклад, нагрівальна піч), в вираз для розрахунку К і Т входитимуть інші фізичні величини, але вигляд рівняння може бути таким же.
В автоматиці найчастіше мають справу з рівняннями в безрозмірному вигляді. Тоді елементи, в яких протікає абсолютно різні фізичні процеси, але мають один і той же вид диференціального рівняння, з точки зору автоматики є однаковими.
Безрозмірна форма диференціального рівняння елемента.
Для запису рівняння в безрозмірному вигляді вибирають базові значення величин, що входять в рівняння. За базове значення приймають задане значення параметра (H0) і максимально можливі зміни приток (витрат).
Введемо безрозмірні значення рівня (# 966;) і витрати на притоці (# 956;)
Тоді рівняння динаміки бака набирає вигляду
Тоді рівняння запишеться у вигляді, загальноприйнятому в теорії автоматичного регулювання
У цьому рівнянні Т. [з] має розмірність часу, тому називається постійної часу. а k - безрозмірний коефіцієнт посилення елемента (коефіцієнт передачі).
Рівняння статики матиме вигляд. з якого .Коеффіціент посилення k показує у скільки разів вихідна величина більше або менше вхідний в статичних режимах роботи.
Можна скласти диференціальне рівняння двох послідовно з'єднаних баків з водою. Тоді виходить диференціальне рівняння другого порядку виду
У цьому рівнянні коефіцієнти при похідних має розмірність часу, тому Т1 і Т2 - постійні часу.
У більш складних елементах можна отримати більш складні диференціальні рівняння, наприклад,
Так як працювати надалі з диференціальнимирівняннями досить незручно і складно, в автоматиці параметри, що залежать від часу t, переводять в площину комплексних чисел, вводячи різні оператори. У площині цих чисел отримують алгебраїчні рівняння, працювати з якими значно простіше. Для перекладу диференціальних рівнянь в площину інших параметрів використовується перетворення Лапласа, але частіше використовується формальний переклад введенням оператора диференціювання.
Запис рівнянь на операційному вигляді.
Використовується формальний переклад диференціальних рівнянь в операційний вид, який повністю збігаються із суворим, з використанням перетворення Лапласа при нульових початкових умовах, що практично завжди виконується в лінійної теорії автоматичного регулювання.
Введемо оператор диференціювання:
Тут р - оператор диференціювання. Тоді записані раніше диференціальні рівняння в операційному вигляді матимуть вигляд:
Ці рівняння алгебраїчні. До них можна застосувати властивості алгебри, наприклад, винести постійний множник # 966; і # 956; за дужки. Отримаємо вищенаведені рівняння в наступному вигляді.
Ці рівняння можна записати в загальному вигляді:
де D (р) - називають власним оператором функції # 966 ;, а k (р) - оператором впливів по # 956 ;.
Тоді в вищенаведених рівняннях (6.12) власні оператори і оператори впливів будуть наступні:
Введемо поняття передавальної функції:
Суворе визначення. Під функцією передачі W (p) розуміють відношення зображення по Лапласа вихідної величини # 966; (p) до зображення по Лапласа вхідний величини m (p) при нульових початкових умовах
Із запису рівняння в загальному вигляді (6.13) слід
З (6.17) випливає, що для знаходження вихідної величини j (р) по заданому вхідному впливу m (р) досить знати передавальну функцію W (р) елемента або системи.
Друге визначення передавальної функції
Під функцією передачі розуміють відношення оператора впливів К (р) і власним оператору функції D (р), отриманими із запису диференціальних рівнянь в операційному вигляді.
Знання передавальних функцій окремих елементів дозволяє отримати передавальні функції різних з'єднань елементів і передавальну функцію системи регулювання.
Передавальна функція різних з'єднань елементів.
Розрізняють три основних види з'єднань: послідовне, паралельне і послідовне з'єднання зі зворотним зв'язком.
1. Передавальна функція послідовно з'єднання елементів
Мал. 14. Послідовне з'єднання елементів
З визначення передавальної функції випливає, що передавальна функція цього з'єднання дорівнює
З цього випливає
Тоді передавальна функція з'єднання буде дорівнює
Отже, передатна функція послідовного з'єднання елементів дорівнює добутку передаточних функцій всіх елементів.
2. Передавальна функція паралельного з'єднання елементів.
При паралельному з'єднанні елементів мають один і той же вхідний сигнал, а вихідні сигнали підсумовуються (рис. 15).
Отже, передавальна функція паралельного з'єднання елементів дорівнює сумі передавальних функцій всіх елементів.
Мал. 15. Паралельне з'єднання елементів
3. Передавальна функція послідовного з'єднання зі зворотним зв'язком.
Розрізняють з'єднання з одиничною і неодиничної зворотним зв'язком.
З'єднання з одиничною зворотним зв'язком.
Мал. 16. Послідовне з'єднання елементів з одиничною зворотним зв'язком
Передавальна функція одиничної зворотного зв'язку дорівнює
Зворотні зв'язку можуть бути позитивними і негативними.
Позитивна - підсилює основний вхідний сигнал: хвх + Хвих
Негативна - послаблює основний вхідний сигнал: хвх - Хвих.
Для отримання передавальної функції цього з'єднання розірвемо зворотний зв'язок, а її дія на разомкнутую систему врахуємо введенням її сигналу на вхід першого елемента (хвх ± Хвих). Отримаємо послідовне з'єднання трьох елементів, передавальна функція якого відома - твір передавальних функцій. За визначенням, передавальна функція замкнутої системи дорівнює
Передавальна функція розімкнутої системи
Звідси можна отримати передавальну функцію замкненої системи:
Знак «-» в знаменнику (6.20) говорить про те, що в системі використана позитивний зворотний зв'язок. При збільшенні вхідного сигналу Хвих буде рости, що суперечить змісту процесу регулювання. Тому для цілей регулювання позитивний зворотний зв'язок не підходить. Вона в основному використовується в різного роду підсилювачах вхідних сигналів.
Знак «+» в знаменнику (6.20) говорить про те, що в системі використана негативний зворотний зв'язок. При збільшенні вхідного сигналу Хвих буде зменшуватися. Отже, негативний зворотний зв'язок використовується в системах регулювання. Тоді передавальна функція системи матиме вигляд
З'єднання з неодиничної зворотним зв'язком (рис. 16.)
Мал. 17. Послідовне з'єднання елементів з неодиничної зворотним зв'язком
Передавальна функція зворотного зв'язку за визначенням
Якщо розімкнути систему, то на вході в елемент 1 буде сигнал. Проробивши те ж саме, що і при одиничної зворотного зв'язку, отримаємо передавальну функцію замкненої системи при негативному зворотному зв'язку у вигляді
Оцінимо вплив зворотного зв'язку на зміну вихідної величини системи Хвих при зміні вхідної величини хвх. розглянувши разомкнутую систему з трьох елементів (6.18) і замкнутої одиничної зворотним зв'язком (6.21) і неодиничної (6.22).
Нехай елементи системи будуть найпростіші, мають передавальні функції, рівні коефіцієнтам підсилення:; ; ; . Тоді в розімкнутої системі (рис.14) вихідна величина буде дорівнює. тобто Хвих при зміні хвх буде істотно змінюватися в До раз ().
У замкнутій системі з одиничною зворотним зв'язком
тобто Хвих буде незначно змінюватися, в порівнянні зі зміною хвх.
У замкнутої систем з неодиничної зворотним зв'язком ()
Змінюючи вплив на систему зворотним зв'язком (k4) в широких межах, можна впливати на зміну вихідної величини Хвих при постійних значеннях k1; k2; k3.
Розглянемо систему автоматичного регулювання (САР) як сукупність об'єкта регулювання і регулятора (рис. 18) по каналу регулюючого впливу mрег
Мал. 18. Система автоматичного регулювання
На підставі формул (6.22) для замкнутої системи регулювання можна записати передавальну функцію
Оскільки об'єкт регулювання має цілком певну передавальну функцію Wоб (р), змінювати яку практично немає можливості, вплинути на поведінку системи регулювання можна лише змінюючи властивості регулятора (змінювати значення Wрег (р)).
Передавальна функція складної системи.
У складних системах можуть зустрічатися різні сполуки елементів. Для визначення передавальної функції складної системи в ній виділяють ділянки з різними сполуками. Використовуючи формули передавальних функцій з'єднань, знаходять їх передавальні функції і підганяють систему під відомий вид - послідовне з'єднання зі зворотним зв'язком.
Мал. 20. Складна система з'єднання елементів
Вважаємо, що передавальні функції W1 ... W15 відомі. Виділимо в цій системі складні сполуки: I, II, і III.
Визначимо передавальні функції цих сполук: WI. WII; WIII.
I - паралельне з'єднання двох ланцюжків елементів: 3 - 4 і 7 - 8
II - з'єднання зі зворотним зв'язком, в яку включений елемент 14
III - паралельне з'єднання елементів 12 і 15
Отримаємо послідовне з'єднання елементів зі зворотним зв'язком, в яку входять.
Передавальна функція складної системи буде дорівнює
де - передавальна функція прямого з'єднання елементів; - передавальна функція назад зв'язку.