Дросельний ефект був виявлений Джоулем і Томсоном досвідченим пу-тем в 1852 р [Дослідами було встановлено, що в результаті дроселювання змінюється температура робочого тіла. Це явище було названо ефектом Джоуля-Томсона. Зміна температури при дроселюванні пов'язано з тим, що в кожному реальному газі діють сили тяжіння і відштовхуючись-ня між молекулами. При дроселюванні відбувається розширення газу, що супроводжується збільшенням відстані між ними. Все це призводить до зменшення внутрішньої енергії робочого тіла, пов'язаного з витратою рабо-ти, що, в свою чергу, призводить до зміни температури.
Температура ідеального газу в результаті дроселювання не змінює-ся, і ефект Джоуля-Томсона в даному випадку дорівнює нулю. Таким чином, зміна температури реального газу при дроселюванні визначається величиною відхилення властивостей реального газу від ідеального, що пов'язано з дією міжмолекулярних сил.
Розрізняють диференційний та інтегральний температурні дросель-ефекти. При диференціальному ефекті Джоуля-Томсона температура змінюється на нескінченно малу величину, а при інтегральному - на конеч-ву величину. Якщо тиск газу зменшується на нескінченно малу вели-чину dp, то відбувається нескінченно мале зміна температури, тобто dTi = ai dpi або
Величина ai називається диференціальним температурним ефектом Джоуля-Томсона. Значення а, можна визначити з рівняння (див. § 5.48)
З огляду на, що при дроселюванні немає зміни ентальпії (di = 0), напів-чим
Дросельний ефект може бути позитивним, негативним і рав-ним нулю. Позитивний дросель-ефект має місце в разі, коли при дроселірованіі температура газу знижується. Негативний - коли по-підвищується. У разі незмінності температури при дроселювання на-блюдается нульовий ефект Джоуля-Томсона. Стан реального газу при дроселюванні, коли дросельний ефект дорівнює нулю, називається точкою інверсії. У цій точці відбувається зміна знака температурного ефекту. Якщо температура газу перёд дросселированием менше температури Інверсія-сії, то газ при дроселюванні охолоджується, якщо більше - то нагрівається.
Для знаходження умов, при яких відбувається зміна температу-ри газу або вона залишається незмінною, необхідно проаналізувати уравне-ня (7.19), записане у вигляді
При дроселюванні dp <0, так как давление газа всегда уменьшается. Теплоемкость ср - величина положительная. Отсюда следует, что знак dT
залежить від знака виразу і завжди йому протилежний.
при T (dv / dT) p - v = 0 dT = 0. Випадок, коли dT = 0 можна використовувати для
отримання температури інверсії ТНН.
Останній вираз називається рівнянням кривої інверсії (кривої, на якій дросельний ефект дорівнює нулю).
Інтегральний ефект Джоуля-Томсона визначається в результаті інтег-рірованія рівняння (7.20)
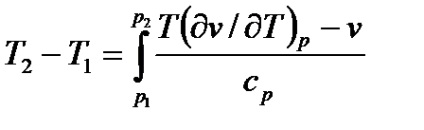
У техніці досить часто доводиться мати справу з газоподібними віщо-ствами, що представляють механічну суміш окремих газів, за своїми властивостями наближається до ідеальних газів.
Наприклад, атмосферне повітря являє газову суміш, включаю-щую азот, кисень, вуглекислий газ, водяні пари і ряд інших газів. Оп-ределение параметрів необхідно для вирішення багатьох практичних завдань.
Газовою сумішшю називається суміш окремих газів, що хімічно не реаг-ючий між собою, тобто кожен газ в суміші повністю зберігає всі свої властивості і займає весь об'єм суміші. Тиск, який створюють молекули кожного окремого газу суміші, за умови, що цей газ знаходиться один в тій же кількості в тому ж обсязі і при тій же температурі, що і в суміші, називається парціальним (частковим) тиском.
Будемо вважати, що кожен окремий газ суміші підпорядковується рівнянню (2.7), тобто є ідеальним газом. Тому параметри газової суміші так само можуть бути обчислені за рівнянням Клапейрона
де всі величини в цьому рівнянні відносяться до суміші газів.
Відповідно до закону Дальтона загальний тиск суміші ідеальних газів дорівнює сумі парціальних тисків газів, що входять в суміш
де р - тиск суміші; парціальні тиску окремих газів суміші.
Газова суміш може бути задана масовими, об'ємними і молярними частками.
Масова частка - відношення маси кожного окремого газу до сумарної масі суміші
Сума масових часток дорівнює одиниці
Об'ємна частка - відношення парціального (наведеного) обсягу каждо-го газу до загального обсягу суміші
газу; V - об'єм суміші газів.
Парціальний об'єм - це об'єм, який займав би газ, якщо б його тиск і температура дорівнювали параметрам суміші газів.
Парціальний об'єм кожного газу при постійній температурі знаходиться за законом Бойля-Маріотта
Склавши ці рівняння почленно, отримаємо, що сума парціальних обсягів по-мов дорівнює обсягу суміші (закон Амага)
Якщо скласти об'ємні частки, то отримаємо
Із закону Бойля-Маріотта (при постійній температурі) слід pi / p-Vi / V. Звідси
Остання формула дозволяє визначати парціальний тиск компо-нентов суміші, якщо відомий її об'ємний склад.
Завдання суміші молярними частками полягає в наступному. Спочатку знаходимо кількість молей кожного компонента суміші за співвідношеннями
де M1. M2. .... Mn - кількість молей кожного компонента; μ1. μ2, ..., μn мо-лекулярние ваги відповідних компонентів суміші.
Звідси вся газова суміш буде містити М молей
Молярний частки yi (i = 1,2,3, ..., n) знаходяться в вигляді відносин
Так як М = m / μ, то молекулярна вага суміші μ буде визначатися за формулою
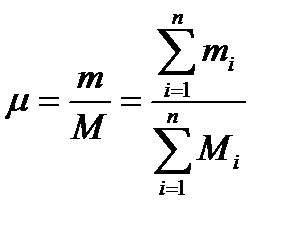
Отримане значення називається середнім удаваним значенням молекулами-лярного ваги суміші. Знання молекулярного ваги дозволяє за формулою (2.9а) R = 8.3143 / μ знаходити газову постійну суміші R (нижче буде приведена формула для визначення μ за відомою R).
Згідно із законом Авогадро молярний обсяги різних газів при однакових тисках і температурах рівні (в рівних обсягах різних газів содер-жится однакову кількість молекул). Звідси для i -го газу суміші справед-ливо співвідношення
де Vμ - обсяг, займаний одним молем газу.
Для всієї суміші отримаємо
Отже, молярний і об'ємні частки чисельно рівні між собою.
Виведемо формулу для визначення молекулярної ваги суміші по її об'єк-емному складу. З попереднього для i -го компонента можна записати
або для всієї суміші
Замінюючи в останньому рівнянні молекулярні ваги їх щільністю (на підставі закону Авогадро), отримаємо
У разі, коли газова суміш задана масовим складом, то з рівняння стану
Для тиску всієї суміші отримаємо формулу
З огляду на, що pV = mRT, отримаємо
За відомою газової постійної суміші, використовуючи формулу (2.9а), мож-но знайти молекулярну масу суміші.