При проектуванні, розробці та оцінці якості будь-яких складних систем, до яких також відносяться і системи програмних продуктів, виникає необхідність виконання системи вельми суперечливих вимог. Якщо ці вимоги до системи вдається висловити у вигляді деякої сукупності приватних кількісних показників (приватних критеріїв - ч-критеріїв), то задача проектування може бути формалізована у вигляді багатокритеріальної векторної задачі математичного програмування (ВЗМП):
де (1) означає, що збільшення будь-якого з r ч-критеріїв покращує якість системи; [1] X = (xj) n - (рішення ЛПР) параметри, керовані особою, яка приймає рішення (ОПР); Dx - область допустимих рішень ЛПР.
Далі будемо вважати, що ч-критерії лінійні, а область замкнута і обмежена лінійними нерівностями. Тоді багатокритерійну (векторна) завдання ЛП (ВЗЛП) запишеться у вигляді:
де в запису справа обмеження представлені у вигляді невід'ємних лінійних функцій (змінних) [2].
ВЗЛП (3), (4) не є оптимізаційної завданням, так як говорити про оптимальність рішення можна тільки в сенсі одного якогось ч-критерію з їх сукупності (3). Стосовно до всієї сукупності (3) можна говорити лише про деяке раціональне, в більшій чи меншій мірі практично прийнятному, компромісному рішенні, при якому, можливо, жоден з r ч-критеріїв не прийме максимальне значення. Пропонуються різні процедури для пошуку раціональних рішень [1-8], проте необхідною умовою для кожного такого рішення є неможливість його поліпшення хоча б по одному ч-критерію, щоб при цьому жоден з решти не зіпсувала свого значення. Таке "неулучшаемое" рішення прийнято називати оптимальним по Парето [1-3], або скорочено П-оптимальним.
Таким чином, рішення будь-якої багатокритеріальної задачі або починається з пошуку всього безлічі П-оптимальних рішень (П-безлічі), де повинно знаходитися і остаточне, компромісне рішення, або закінчується перевіркою попередньо отриманого рішення на П-оптимальність і, якщо буде потрібно, його наступним поліпшенням з якихось ч-критеріїв без погіршення значень інших.
Основною метою даної роботи є формулювання досить простого і легко формалізуються алгоритму, що дозволяє визначити:
- все безліч Парето-оптимальних рішень ВЗЛП (Dpx);
- чи є рішення X ¢ П-оптимальним і, якщо буде потрібно, знайти найближче до нього П-рішення.
В основу запропонованого методу покладено формальна умова П-оптимальності рішення X ¢ [1; 2]: рішення X ¢ÎDx П-оптимально, якщо не існує такого іншого рішення XÎDx, при якому б виконувалися умови:
"K: Lk (X) ³Lk (X ¢), т.е.Dk = Lk (X) -Lk (X ¢) ³0, (5)
при цьому хоча б одне з них - строго (Dk1> 0).
Для формулювання алгоритму умови (5) зручно представити у вигляді завдання ЛП (ЗЛП):
при обмеженнях Dk = Dk (X) ³0, "k = 1; r. (7)
Умови (7) в геометричному сенсі - це деяка область, утворена перетином r n-мірних напівпросторів, заданих нерівностями (7). У разі сумісності система (7) утворює деякий простір - конус з вершиною X ¢. Кожна точка цього конуса є поліпшеним, в порівнянні з X ¢, рішенням (надалі цей конус називається конусом домінування, д-конусом).
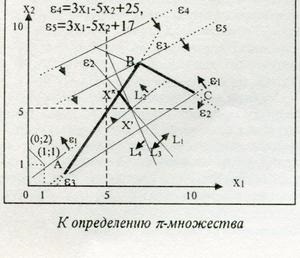
До визначення p-безлічі
На малюнку частина цього конуса, розташована в області Dx, показана відрізком X ¢, Xp для наступної ВЗЛП:
L2 (X) = - x1 + x2 + 10, ® max e2 = -x1-4x2 + 34, Dx
L3 (X) = - x1-x2 + 16, X e3 = 2x1-x2-5,
L4 (X) = - 2x1-x2 + 30, (8) "i, j: xj, ei³0. (9)
Виродженість д-конуса обумовлена повною протилежністю ч-критеріїв L1 і L3 - їх вектор-градієнти відрізняються тільки знаками. Фізично такий випадок не може мати місця, тому що якщо, наприклад, L1 вимагає максимізації надійності системи, то L3 - мінімізації тієї ж надійності. Однак формальний розгляд такої системи ч-критеріїв не втрачає сенсу.
Зміщуючи точку X ¢ всередину д-конуса, отримаємо краще рішення. Таке поліпшення (в даному випадку по ч-критерію L2) можливо аж до зміщення в точку Xp, коли весь д-конус, крім його вершини, опиниться поза області Dx. Оскільки вибір точки X ¢ ніяк не впливає на форму і орієнтацію д-конуса (відповідає його паралельного переносу в n-вимірному Октант), то можна, вибираючи X ¢ в різних точках Dx, помітити, що всі П-множство складуть точки, розташовані на ребрах (гранях) АВ і ВС малюнка.
Таким чином, з рішення ЗЛП (6), (7) при будь-якому виборі вершини д-конуса X ¢ в позитивному Октант [3] випливають висновки: якщо Dmax> 0, то д-конус існує, а П-безліч складуть деякі грані безлічі Dx; якщо Dmax = 0, то система (7) сумісна тільки в точці X ¢, а значить, будь-яка точка X ¢ÎDx П-оптимальна (Dpx = Dx).
У разі Dmax> 0 точка X ¢ повинна послідовно вибиратися на кожній з граней області Dx. Це рівносильно додаванню до системи (7) ще одного нерівності, відповідного i-ой межі (ei³0). Якщо в ході рішення ЗЛП критерій D (6) збільшиться, то дана грань не є П-оптимальної, а якщо Dmax = 0 - грань увійде в безліч Dpx. Перевіривши всі m граней симплекса Dx, знайдемо П-безліч Dpx.
Перенесення безлічі (6) на межі Dx пов'язаний з додатковими розрахунками, тому вершину X ¢ д-конуса доцільно вибрати в фіксованій точці X ¢ = (1) [4] і в цю ж точку переносити межі симплекса Dx. Тоді, опускаючи елементарні перетворення, наведену до точки X ¢ = (1) n ЗЛП (6), (7) запишемо у вигляді:
Перетворені межі симплекса при цьому запишуться:
Проілюструємо процес вирішення на прикладі (8), (9). Згідно (10) - (11) запишемо ЗЛП в систему (12) в алгебраїчному і табличному вигляді T1:
T1 x1 x2 1 T2 x1 D1 1 T3 e2 D1 1
D = -3x1 + 3®max, D -3 0 3 D -3 0 3 D -1 -4 0
D1 = x1 + x2-2, D1 1 1 -2 x2 -1 1 2 x2 1
D2 = -x1 + x2, D2 -1 1 0 D2 -2 1 2 D2 0
D3 = -x1-x2 + 2, D3 -1 -1 2 D3 0 -1 0 D3 0 (13)
D4 = -2x1-x2 + 3, D4 -2 -1 3 D4 -1 -1 1 D4 0
e1 = -5x1 + 7x2-2, e1 -5 7 -2 e1 -12 7 12 e1 0
e2 = -x1-4x2 + 5, e2 -1 -4 5 e2 3 -4 -3 x1 1
e3 = 2x1-x2-1. e3 2 -1 -1 e3 3 -1 -3 e3 0
Методом послідовного поліпшення планів [6; 7] вирішується ЗЛП, отчеркнуть в T1 подвійний лінією. Обмеження ei, записані під подвійною лінією просто перераховуються за формулами звичайних Жорданових винятків (очіку). Після кроку ожі (заміна D1 «x2, T1) отримано оптимальне рішення. Так як Dmax¹0 (Dmax> 0), то д-конус існує і, отже, p-безліч складуть деякі грані області D х. Ці межі визначається шляхом виключення тих граней, які не можуть увійти в D х. Для них при D> 0 маємо ei³0 (грань e1). Номери i залишилися граней утворюють безліч I- =. Послідовна перевірка граней iÎI- виявляє межі epi. Так, наприклад, додавши до системи (11) грань e2<0, после шага ОЖИ (e2«х1,Т2) получим решение X0=(1;1) и Dmax=0, из чего следует p-оптимальность грани e2 области Dх. То же для e3 (см.рис.).
Щоб Dpх вберегти від хибних рішень, з системи (4) повинні бути виключені межі, що не утворюють кордонів області D х. Для цього послідовно "ei³0 замінюється кордоном ei = 0. Якщо при цьому система (4) стає несумісною, то нерівність ei³0 виключається. Виключаються і лінійно залежні нерівності (див. Рис. E4, e5) [5]. Вважаючи, що такий відсів виконаний , запишемо порядок вирішення завдання.
Алгоритм 1 визначення p-безлічі
20. Вирішити ЗЛП (10), (11), попутно перераховуючи (12)
30. Якщо Dmax = 0, писати Dpх = D х, йти до 110
40. Виключити з (12) обмеження ei³0, записати (уточнити) безліч I - =
50. Якщо I- = 0, йти до (100)
60. Включити грань ei, iÎI- в систему (11) і вирішити ЗЛП (10), (II) + ei
70. Якщо Dmax¹0, i виключити з I-, йти до 40
80. Включити грань ei в Dpх (ei = epi), i виключити з I-
90. Якщо I-¹0, йти до 60
Якщо Dpх знайдено, то питання про приналежність йому деякої довільної точки Х ¢ зводиться до підстановці її компонент х ¢ j в (9) і обчисленню невязок ei. Якщо при невід'ємності всіх невязок хоча б одна з них, які відповідають П-безлічі, дорівнює нулю, то Х ¢ÎDpх.
Однак для перевірки П-оптимальності Х ¢ немає необхідності будувати все П-безліч. Досить вирішити ЗЛП (6), (7), (4). Якщо Dmax = 0 - точка Х ¢ П-оптимальна. При Dmax¹0 буде знайдено покращене рішення (див. Рис. Х ¢ і ХP).
В [8] показано, що П-безліч ВЗЛП може бути знайдено як безліч рішень ЗЛП при обмеженнях (4) і з цільовою функцією, отриманої як лінійна комбінація ч-критеріїв: [6]
при всіляких значеннях вагових коефіцієнтів ч-критеріїв - ak.
Недолік такого підходу полягає в тому, що можуть бути виявлені тільки П-рішення, що лежать на кордонах області D х. В [2] для випадку Dpх = D х пропонується вибір такого вектора коефіцієнтів ao = (ak), який все коефіцієнти cj в "згортку" (14) звертає в нуль. Такий підхід може ввести неправдиві П-рішення. Наприклад, взявши ao = (0,5; 0; 0,5; 0) для системи (8), слід було б зробити висновок, що Dpх = D х, але з малюнка видно, що це не так.
Зазначимо обчислювальну процедуру, що реалізує принцип "згортки" і дозволяє усунути зазначений недолік. Суть методу полягає в тому, що для виявлення П-рішень, розташованих на i-ой межі (4), необхідно шляхом вибору вектора ai виконати дві умови: коефіцієнти cj (14) і aij i-ой межі повинні бути пропорційні при кожному j; ці коефіцієнти повинні мати різні знаки, що забезпечить екстремальне значення "згортки" на i-ой (i = 1; m) межі. Вважаючи коефіцієнт пропорційності hi позитивним, ці умови з урахуванням (14) запишуться у вигляді:
Для i-ой межі далі складається система рівності (16), рішення якої дозволяє встановити, чи існує при hi> 0 вектор ai = (aik), який реалізує необхідні умови для цієї межі.
Зазначена раніше некоректність формально пов'язана з тим випадком, коли hi = 0 в (16). Для її усунення досить випадок Dpх = D х зв'язати з тією ситуацією, коли всі m граней СІМПЕКС D х будуть включені в П-безліч. Це виявиться після перевірки всіх m граней. Таким чином, визначення П-безлічі при даному підході зводиться до m-кратному рішенням системи (16), або, точніше, до вирішення ЗЛП: [7]
де Oj - змінні, які повинні бути звернені в нуль (нульові змінні); hi - коефіцієнт пропорційності.
Слід зазначити, що як в першому, так і в другому випадку доводити рішення ЗЛП до кінця, як правило, не має сенсу. Достатньо лише переконатися, що D> 0 (1-ий алгоритм) або hi> 0 (2-ий алгоритм), що гарантує від помилкового висновку про неоптимальности перевіряється межі.
Алгоритм 2 визначення p-безлічі
30. Вирішити ЗЛП (17), (18) (maxh)
40. Якщо hmax £ 0, виключити грань ei, йти до 60
50. Писати ei = epiÎDpх
80. Якщо | Dpх | ¹m, йти до 100
90. Писати Dpх = D х
Отримані відповідно до наведеного алгоритмом рішення наступні:
h1max = 0, (АС); h2 = 0,1, (ВС); h3 = 1/7, (АВ). (19)
Як видно з (19), грань АС не входить в П-безліч (h1max> 0).
При однаковій обчислювальної нескладності обох алгоритмів, тільки до першого підходу притаманні такі три особливості:
- існує можливість перевірити П-оптимальність будь-якого рішення Х ¢ÎD х, а для ВЗЛП і знайти найближче П-оптимальне, не вдаючись до пошуку всього П-безлічі;
- випадок Dpх = D х виявляється на самому початку розрахунків, після чого необхідність в обчисленні відпадає;
- без додаткових складнощів існує можливість перевірити П-оптимальність деякої довільної точки Х ¢ÎD х в загальному завданню МП (1), (2).
В останньому випадку досить як масиву вихідних даних || Сkj || використовувати матрицю значень похідних в точці Х ¢ÎD х (апроксимація):
Відповідь, що отримується в формі "так", "ні", не містить вказівок (в разі «ні») про направлення подальшого пошуку П-оптимального рішення. У разі «так» можна говорити тільки про локальну П-оптимальності рішення разом з проблемами, властивими пошуку глобального екстремуму або П-множини. Проте залишається можливість пошуку П-рішень шляхом упорядкованого перебору точок ХÎD х, наприклад по вузлах числовий решітки або методом випадкового пошуку.
На закінчення відзначимо, що якщо у вихідній ВЗЛП є m1 обмежень-рівностей, то, записавши їх в канонічному вигляді не більше ніж за m1 кроків ожі (можуть виявитися лінійно залежні), ВЗЛП приводимо до виду (3), (4), але з зменшеним на m1 числом вільних змінних.
1. Дубов Ю.А. Травкин С.І. Якимець В.М. Багатокритеріальні моделі формування та вибору варіантів систем. - М. Наука, 1986. - 295 с.
2. Подиновский В.В. Ногін В.Д. Парето-оптимальні рішення багатокритеріальних задач. - М. Наука, 1982. - 256 с.
3. Ларичев О.І. Поляков О.А. Людино-машинні процедури прийняття рішень багатокритеріальних задач МП: (Огляд). Економіка і математичні методи. - 1980. - т.16, вип. 1. - С. 127-145.
4. Гермейера Ю.Б. Введення в теорію дослідження операцій. - М. Наука, 1972. - 383 с.
6. Юдін Д.Б. Гольштейн Є.Г. Завдання і методи лінійного програмування. - М. Сов. радіо, 1969. - 736 с.
7. Берзін Е.А. Оптимальний розподіл ресурсів і теорія ігор. - М. Радіо і зв'язок, 1983. - 183 с.
8. Карлін С. Математичні методи в теорії ігор, програмуванні та економіці. - М. Мир, 1964. - 838 с.