Залежність небезпеки відмов від часу очевидно може бути трьох типів:
1. Небезпека відмов зі збільшенням часу експлуатації убуває.
Елемент в процесі експлуатації покращує свої надежностние характеристики. Цей рідкісний випадок має місце, наприклад, в процесі попередньої підробітки, коли в початковий період експлуатації відмовили, браковані елементи замінюються новими. Сформована так партія елементів покращує свої характеристики надійності.
2. Небезпека відмов зі збільшенням часу експлуатації збільшується. Елемент в процесі експлуатації погіршує свої характеристики надійності. Елемент «старіє». Це очевидний, найбільш поширений випадок.
3. Небезпека відмов в процесі експлуатації не змінюється, залишається постійною. Елемент в процесі експлуатації «не старіє», залишається «новим». Очевидно, що це якась теоретична модель.
Розглянемо докладніше останній випадок. якщо # 955; (t) = const, то згідно (1.10) отримаємо
Отриманий закон надійності називається експоненціальним і має велике значення в теорії надійності. Частота відмов відповідно до (1.3) дорівнює
Середнє напрацювання на відмову відповідно до (1.11) дорівнює
Обчислимо ймовірність надійної роботи на інтервалі, рівному середньому часу відмов t = T0.
Надійність дуже мала, приблизно лише третина елементів залишиться працездатними. Тому для відповідальних елементів час експлуатації слід вибирати багато менше середнього часу життя елемента (t < а ймовірність відмови приблизно дорівнює Імовірність відмови на малому інтервалі часу # 8710; t у справного елемента дорівнює # 955; # 8710; t. Ця ймовірність не залежить від відпрацьованого часу, якщо елемент справний, то його подальша поведінка не залежить від минулого передісторії. Вірно і зворотне твердження. Для моделей відмов, коли передісторія не впливає на поведінку відмов, справедливий експонентний закон надійності. Такі моделі відмов називаються схемою миттєвих пошкоджень.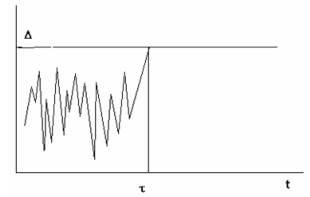
Рис.2.1 Модель миттєвих пошкоджень.
Нехай на елемент впливає випадкова ударна перевантаження (рис 2.1). Коли вона менше критичної # 8710 ;, відмови немає, немає ніяких дрібних пошкоджень, що погіршують надежностние характеристики. Елемент залишається за всіма показниками як «новий». Як тільки перевантаження перевищує критичний рівень, елемент відмовляє. Якщо перевантаження являє собою випадковий процес типу білого шуму, все відліки якого незалежні, передісторія експлуатації на момент відмови не впливає. Тобто така модель відмови відповідає експоненціальному закону надійності.
Недолік експоненціального закону в тому, що він відображає рідко зустрічає модель відмов. Однак далі буде показано, що тільки цей закон дозволяє побудувати практично застосовні, інженерні методи розрахунків.
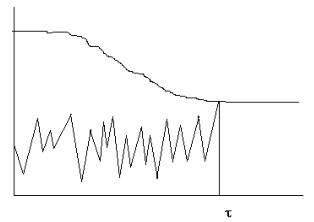
Рис.2.2. Схема зі змінним порогом.
Розглянемо ще одну схему миттєвих ушкоджень, але зі змінним у часі порогом (рис. 2.2). Ця схема відрізняється від схеми, наведеної на рис 2.1 тим, що поріг - межа допустимих перевантажень змінний. Спочатку він великий і перевантаження ніколи не може його досягти. Потім поріг знижується і в певний момент часу t0 фіксується на деякому постійному значенні, яке досягається перевантаженням.
Маємо при t При t> t0 маємо експонентний закон надійності P (t) = e - # 955; (t- t0) Графік ймовірності безвідмовної роботи показаний на рис. 2.3. 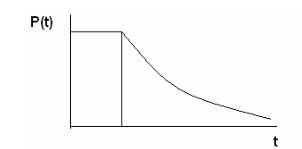
Рис.2.3. Закон зі змінним порогом.
Для щільності ймовірності відмови маємо (див. Рис. 2.4):
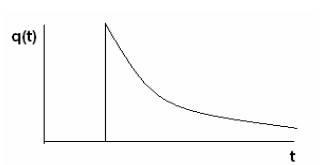
Рис.2.4. Небезпека відмови.
Ця модель може служити наближенням для результатів експериментального визначення закону надійності, отриманого у вигляді, показаного на рис. 2.5.
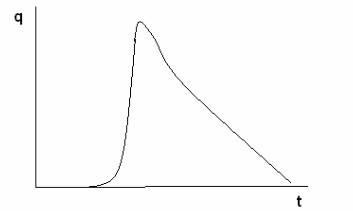
Рис.2.5. Експериментальна крива частоти відмов.
1. Що таке експонентний закон надійності?
2. У якому співвідношенні знаходяться середній час безвідмовної роботи і реальний час експлуатації?
3. Опишіть модель миттєвих пошкоджень.
3. Модель накопичення пошкоджень. Гамма - розподіл часу безвідмовної роботи
Модель накопичення ушкоджень передбачає, що дія збурень в процесі експлуатації, знос елемента весь час накопичується, збільшується. Це накопичення може починатися від різних початкових умов через випадкових дрібних дефектів виробництва, може наростати з різною швидкістю через випадкового характеру впливів і т. Д.
Припустимо, що існує певний постійний поріг, після досягнення якого відбувається відмова (рис.3.1).
Рис.3.1. Модель накопичення пошкоджень.
Розглянемо наступну модель накопичення пошкоджень (рис 3.2).
Рис.3.2. Прийнята схема накопичення пошкоджень.
У випадкові незалежні моменти часу стрибком відбувається збільшення пошкодження. Всі скачки рівні по амплітуді. Приймемо величину стрибка, яка дорівнює a. Приймемо також, що співвідношення між стрибком і порогом таке, що відмова відбудеться після r стрибків. Нехай часи стрибків утворюють найпростіший потік подій, тобто задовольняють таким умовам: події незалежні; потік стаціонарний; в один момент часу може статися тільки один стрибок. Відомо, що для найпростішого потоку або потоку Пуассона, ймовірність настання точно k подій за час T дорівнює
тут # 945; - середня частота стрибків.
Відмова настане після деякого цілого числа стрибків r. Тоді P (t) - функція надійності є ймовірність того, що за час t відбудеться менше ніж r стрибків
Знайдемо щільність ймовірності відмов для такого розподілу
Отримано двухпараметрический (# 945;, r) закон надійності, яким можна було б апроксимувати експериментальні характеристики. Але для цього треба поширити (3.3) на безперервні значення r. В принципі в (3.3) r може бути безперервним всюди крім аргументу факторіала.
Існує гамма-функція, яка для цілих позитивних значень аргументу збігається зі значенням факторіала, і може бути прийнята як поширення поняття факторіала на нецілі значення аргументу.
Вираз для гамма-функції є
Для цілих позитивних r значення гамма-функції дорівнює
Замінюючи в (3.3) факторіал на гамма-функцію, отримаємо
Тоді для безперервних значень r ймовірність відмов дорівнює
а функція надійності дорівнює
Для середнього напрацювання на відмову маємо
Тут зроблена підстановка x = # 945; # 964 ;, отже d # 964; = dx / # 945 ;.
Для гамма-функції має місце рекурентне співвідношення, яке випливає з (3.5):
Тоді для середнього часу життя з (3.9) маємо:
Звернемо увагу, що отриманий результат узгоджується з результатами для експоненціального закону. Для моделі миттєвих пошкоджень досить одного події - досягнення порогу (r = 1), яке не залежить від передісторії процесу, щоб відбулася відмова. Середня частота подій в пуассоновском потоці # 945; по ймовірності дорівнює величині, зворотній середньому часу між відмовами 1 / T0e для експоненціального закону надійності. отже,
Тоді для експоненціального закону з (3.11) отримуємо відомий нам результат
Для дисперсії часу життя маємо
Тут враховано, що згідно (3.10)
Небезпека відмови дорівнює:
Небезпека відмови для цього закону надійності обчислюється складним чином. Однак при малих часах можна прийняти P (t) ≈1; e - # 945; t ≈1, тоді з (3.6) випливає, що залежність небезпеки відмови від часу має вигляд # 955; (t) ≈At r -1. що дозволяє оцінити поведінку небезпеки відмови на початковому інтервалі. Точні залежності показані на рис 3.3.
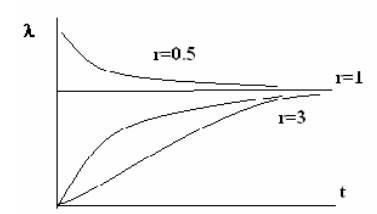
Рис.3.3. Залежність небезпеки відмов від параметра.
При r> 1 маємо модель старіючих елементів (небезпека відмов збільшується). При r = 1 маємо експонентний закон надійності. Це відповідає моделі миттєвих пошкоджень. Одного стрибка досить для відмови. при r<1 имеем убывающую опасность отказа. Частота отказов представлена на рис.3.4. В пределе при r→∞ закон гамма- распределения стремится к нормальному закону надежности.
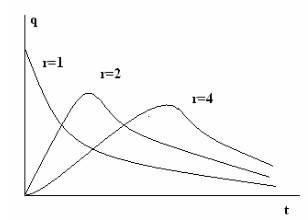
Рис.3.4. Щільність ймовірності відмов - частота відмов.
1. Опишіть модель пошкоджень закону гамма-розподілу часу безвідмовної роботи?
2. Ч то таке гамма-функція, навіщо вона використовується при описі закону гамма-розподілу?
3. Який вигляд має залежність небезпеки відмови від часу при законі гамма-розподілу?