Ентропія і ймовірність стану
Відомо, що будь-яка система без впливу на неї ззовні прагне прийти в стан, що характеризується мінімумом її потенційної енергії. Ця інформація дозволяє в деякій мірі прогнозувати напрямок протікання того чи іншого процесу в природних умовах "без впливу на тіло або систему ззовні. Крім того, як показав Клаузиус, реальні процеси завжди розвиваються таким чином, що одна з найважливіших характеристик стану системи - ентропія - зростає . Отже, будь-яка термодинамічна система буде розвиватися в напрямку мінімуму потенційної енергії і максимуму ентропії. Але не тільки потенційна енергія і ентропія можуть допомогти в определени напрямку протікання реальних процесів. Існує ще один, статистичний, закон природи, в якому стверджується, що найбільш імовірним є стан з максимальним безладдям.
Розглянемо посудину, що складається з декількох з'єднаних між собою осередків. Помістимо в цю посудину n молекул, які можуть вільно переміщатися по судині з комірки в комірку, розподіляючись яким завгодно чином. Характер цього розподілу може бути найрізноманітнішим. Як приклад розглянемо розподіл шести молекул в посудині з трьох осередків. Нескладні міркування переконають нас у тому, що можливі різні способи розподілу молекул по осередках, частина яких показана на малюнку 9. Як приклад розглянемо таку ситуацію. Ящик розділений перегородками на три відсіки. Нехай в одному з них знаходяться молекули; два інших - порожні. Таку систему частинок можна вважати впорядкованим. Прибравши перегородки між відсіками, ми помітимо, що молекули, беручи участь в хаотичному тепловому русі, через деякий час займуть весь наданий їм об'єм. Спостерігаючи далі, ми побачимо, що молекули перераспределились так, що в кожному з відсіків міститься приблизно однакове число молекул, хоча неминучі і деякі відхилення - флуктуації, які будуть тим менше, чим більше вихідне число молекул в ящику. Таким чином, система, надана сама собі, приходить в найбільш ймовірне стан: однакове число молекул в кожному відсіку. Цей процес перерозподілу розвивається в такому напрямку, завдяки якому ентропія зростає; при цьому система приходить до найбільш вірогідного стану. Інакше, зростання ентропії пов'язане зі збільшенням імовірності стану. Кількісною характеристикою ймовірності того чи іншого стану є термодинамічна ймовірність, яка являє собою не що інше, як число способів, якими може бути реалізовано стан даної фізичної системи. Розподіл, відповідне малюнку 9, є найбільш вірогідним.
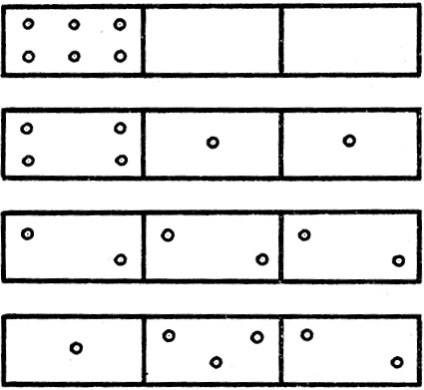
Мал. 9. Способи розподілу молекул по осередках
Вивчаючи термодинамічні процеси, Больцман зауважив спільність у напрямку зміни ентропії деякої системи і в значенні термодинамічної ймовірності стану. Він встановив, що ентропія деякої термодинамічної системи пропорційна логарифму ймовірності її стану. Підвищення ентропії означає порушення впорядкування, прагнення системи до хаотичного руху частинок, що її утворюють. Згідно з теоретичними дослідженнями Больцмана
Згідно з теоретичними дослідженнями Больцмана (34)
де S - ентропія системи; W - термодинамічна ймовірність її стану.
Розвиваючи далі уявлення Больцмана про зв'язок ентропії та ймовірності стану, німецький фізик М. Планк знайшов коефіцієнт пропорційності в співвідношенні (34) і отримав рівність
Коефіцієнт пропорційності (35)
де k - константа, яка отримала згодом назву постійної Больцмана.
З робіт Больцмана і Планка слід, що другий початок термодинаміки, так само як і перше, є статистичними законом. Другий закон термодинаміки справедливо тільки для великого числа молекул, до якого можна застосувати статистичні методи. Встановлений Клаузиусом закон зростання ентропії слід розуміти як середньостатистичний висновок. В окремих частинах системи можуть протікати процеси, що розвиваються так, що ентропія цієї частини системи може спадати, хоча в цілому макросистема характеризується зростанням ентропії. Ці флуктуації енергії, щільності, температури безперервно виникають і зникають через порівняно малі проміжки часу. Найбільш ймовірне стан означає те, що система знаходиться в стані термодинамічної рівноваги. Співвідношення між ентропією і термодинамічної ймовірністю дозволяє стверджувати, що ентропія є мірою близькості ізольованої системи до стану термодинамічної рівноваги.