При передачі даних по радіоканалу дуже гостро постає необхідність звуження спектра сигналів. У попередній статті ми розглянули BPSK модуляцію і приводили спектр BPSK сигналу. Однак на практиці в ефірі побачити подібний спектр з безліччю бічних пелюсток навряд чи вдасться, оскільки ефір - він один на всіх, і розмножувати бічні пелюстки спектру це дороге задоволення. У даній статті ми розглянемо шляхи звуження смуги BPSK сигналу за допомогою формують фільтрів. Ми вже звужували спектр GMSK сигналу за допомогою гауссова фільтра. і говорили про те, що при цьому виникає міжсимвольні інтерференція. У даній статті ми більш уважно розглянемо цей ефект і навчимося так звужувати спектр сигналу, щоб виключити негативний вплив межсимвольной інтерференції.
Міжсимвольні інтерференція і формує фільтр
При розгляді BPSK сигналів ми говорили про те, що в якості вихідного сигналу, що модулює виступає послідовність прямокутних біполярних імпульсів, причому імпульс позитивної амплітуди відповідає переданої одиниці, а негативний - нулю, як це показано на малюнку 1 для вхідного бітового потоку «10110100. ».
Малюнок 1: Послідовність біполярних імпульсів
Однак такий сигнал, що модулює є ідеальним і володіє спектром, з дуже низькою швидкістю загасання бічних пелюсток. Спектр BPSK сигналу на основі сигналу, що модулює показаний на малюнку 2, володіє шириною головної пелюстки (де - швидкість передачі цифрової інформації (біт / c)), рівнем максимального бічного пелюстка -13 дБ, і швидкістю загасання бічних пелюсток як.
Малюнок 2: Спектр BPSK сигналу
Якщо ж ми обмежимо смугу вихідного сигналу, що модулює, це в свою чергу призведе до більш компактному спектру BPSK, але в результаті фронти імпульсів розширяться і отримаємо таку картину (малюнок 3).
Малюнок 3: міжсимвольні інтерференція при згладжуванні фронту імпульсу
Згладжування фронтів призводить до того, що наступний і попередній імпульси починають перекриватися в часі, і стрибок переходить в безперервну криву. При згладжуванні попередній імпульс починає впливати на наступний, а наступний на попередній і обидва спотворюються (заштрихована область на малюнку 3). Цей ефект називається межсимвольной інтерференцією (МСІ, в англомовній літературі intersymbol interference ISI), він погіршує якість передачі інформації, але дозволяє більш компактно представити сигнал в частотній області.
Ми вже вдавалися до згладжування імпульсів, коли розглядали GMSK модуляцію. Для того щоб зробити згладжування фронтів імпульсів необхідно обмежити смугу, іншими словами зробити фільтрацію. Тоді вихідний сигнал, що модулює можна уявити як вихід формує фільтра з імпульсною характеристикою. Фільтр повинен порушуватися сигналом відповідним переданої інформації як це показано на малюнку 4.
Малюнок 4: Яка Формує фільтр, що порушується імпульсами переданої інформації
Пояснимо. Сигнал - набір дельта-імпульсів, віднесених до центру інформаційного імпульсу, віддалених на тривалість інформаційного імпульсу (верхній графік, сірим показана вихідна інформаційна послідовність біт):
де, якщо - перший інформаційний біт дорівнює 1 і, якщо - перший інформаційний біт дорівнює 0. Тоді пропустивши сигнал через фільтр з імпульсною характеристикою, отримаємо сигнал, що модулює, як згортку і:
Таким чином, повністю визначається імпульсною характеристикою і переданої інформацією. Це дуже важливо, оскільки у випадку з BPSK повністю визначає спектральні характеристики сигналу (нагадаємо, що BPSK є виродженим видом модуляції, що збігається з балансної АМ). Значить висновок який ми повинні зробити наступний: змінюючи імпульсну характеристику формує фільтра ми можемо звужувати або розширювати смугу BPSK сигналу.
Яка Формує фільтр Найквіста для усунення МСІ
У цьому параграфі ми розглянемо якими властивостями повинна володіти, щоб забезпечити мінімальну ширину смуги переданого сигналу. Для початку розглянемо більш уважно. Сигнал є послідовність дельта-імпульсів, що відповідають біт переданої інформації і віддалених один від одного на інтервал.
Тоді їх можна трактувати як дискретні відліки сигналу, взяті з частотою. При проходженні формує фільтра дуже важливо, щоб в моменти (т. Е. В вузлах дискретизації) дорівнювало, як це показано на малюнку 5.
Малюнок 5: Виключення МСІ при декодуванні
Тоді при демодуляції і декодування можна виключити вплив МСІ, якщо робити оцінку переданого біта точно в моменти часу, де точно відповідає переданої інформації для всіх біт. Іншими словами вносячи спотворення у вихідний сигнал, що модулює з метою звуження його смуги ми тим не менше, залишаємо в певні моменти часу його значення незмінними і рівними (значенням переданої інформації), щоб на приймальній стороні в ці моменти декодувати без спотворень.
Розглянемо якими властивостями повинна володіти, щоб. Виходячи з (3) можна записати:
Графічно умова (6) показано на малюнку 6.
Малюнок 6: Умови імпульсної характеристики формує фільтра для виключення МСІ при декодуванні
Зрозуміло можна підібрати нескінченне число імпульсних характеристик, які будуть проходити через зазначені точки, але нам потрібна одна, яка буде при цьому забезпечувати мінімальну ширину смуги сформованого сигналу. Такий імпульсною характеристикою формує фільтра є
показана на малюнку 7 (верхній графік), яка відповідає ідеальному ФНЧ з смугою (нижній графік).
Малюнок 7: Імпульсна характеристика ідеального формує фільтра
Імпульсна характеристика (7) є фізично нездійсненною, зважаючи на нескінченних «хвостів» згасаючих в часі як, але вона дозволяє сформулювати теоретичну межу передачі інформації без МСІ. Так при передачі по каналу зв'язку цифрової інформації зі швидкістю без МСІ потрібна смуга. Або як ще кажуть, для передачі інформації без МСІ потрібно не менше 1 Гц смуги на 1 біт / с швидкості передачі інформації. Наприклад в смузі 1 МГц без МСІ можна передати цифровий потік зі швидкістю не більше 1 Мбіт / c.
Сигнал на виході формує фільтра можна уявити як відгук формує фільтра на вхідні дельта-імпульси відповідні вхідному битовому потоку, що наочно показано на малюнку 8.
Малюнок 8: Яка Формує фільтр як інтерполятор
На верхньому графіку малюнка 8 кожен символ інформації множиться на імпульсну характеристику (7), тоді в вузлах дискретизації імпульсні характеристики від інших інформаційних імпульсів дорівнюють нулю і МСІ в моменти взяття відсутня. По суті ми отримали інтерполятор у вигляді ідеального ФНЧ, який «з'єднує» плавною кривою, при цьому самі не спотворює.
Фізично-реалізований формує фільтр «піднесеного косинуса»
Як ми вже говорили вище, імпульсна характеристика (7) нереалізована. Тому на практиці нескінченну доводиться усікати по тривалості, при цьому формує фільтр перестає бути ідеальним інтерполятором. На малюнку 9 показано усічена імпульсна характеристика формує фільтра в залежності від нормованого часу (відповідає одному символу, що передається). Імпульсна характеристика усічена до 4-х символів переданої інформації, т. Е. При. Також на малюнку 9 показаний квадрат АЧХ формує фільтра відповідного усіченої. АЧХ будувалася в залежності від нормованої частоти.
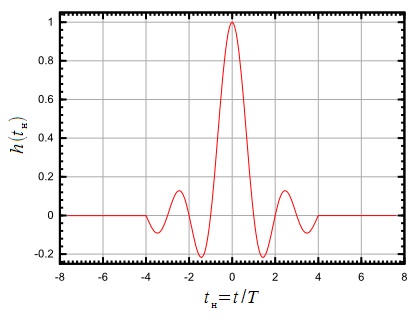
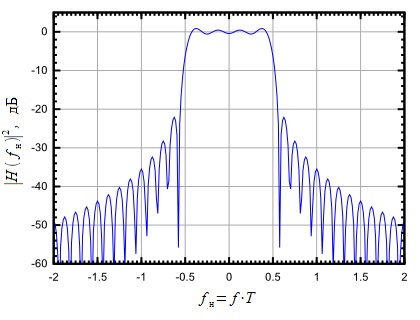
Малюнок 9: Усічена імпульсна характеристика і АЧХ формує фільтра
Як видно з малюнка 9 усічення імпульсної характеристики призводить до появи бічних пелюсток в АЧХ формує фільтра. При цьому рівень бічних пелюсток виходить дуже високим, а швидкість спаду дуже низькою. Крім того з'являється нерівномірність в смузі пропускання фільтра. Цей ефект називається ефектом Гіббса. Для його зменшення Найквистом було запропоновано провести згладжування фронту АЧХ ідеального фільтра, розширивши його, але на відміну від усічення це розширення смуги фільтра можна зробити регульованим, як це показано на малюнку 10.
Малюнок 10: Яка Формує фільтр Найквіста при апроксимації фронту АЧХ піднесеним косинусом
АЧХ фільтра стає кусочной і описується виразом:
Поблизу фронту ідеальна АЧХ апроксимується функцією піднесеного косинуса. Параметр, який змінюється від 0 до 1 задає інтервал на якому відбувається апроксимація. При маємо ідеальний ФНЧ, при маємо формує фільтр з АЧХ у вигляді піднесеного косинуса:
Згладжування фронту в частотної області відповідно до теореми про згортку відповідає множенню імпульсної характеристики (7) на вагове вікно:
На малюнку 11 показані імпульсні характеристики фільтра Найквіста при різному, в залежності від нормованого часу а також їх АЧХ в залежності від нормованої частоти.
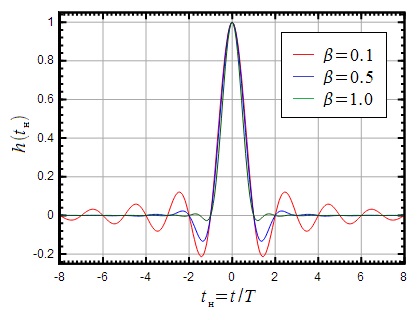
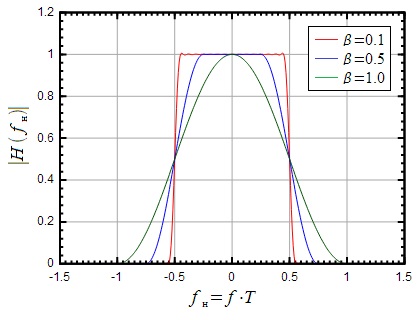
Малюнок 11: Імпульсна характеристика і АЧХ фільтра Найквіста
З малюнка 11 видно, що регулює ступінь згладжування фронту АЧХ ідеального фільтра, що відповідає рівню бічних пелюсток імпульсної характеристики. При АЧХ фільтра набирає вигляду піднесеного косинуса, а імпульсна характеристика має мінімальні бічні пелюстки. Можна помітити, що смуга фільтра Найквіста за рівнем 0.5 (-3 дБ) залишається постійною і дорівнює.
Яка Формує фільтр для узгодженого прийому сигналів. Фільтр «корінь з піднесеного косинуса»
На малюнку 12 показана укрупнена схема системи передачі цифрової інформації.
Малюнок 12: Укрупнення структурна схема системи передачі інформації
На практиці прийом і декодування, як правило здійснюється за допомогою узгодженого фільтра. припустимо, що модулятор і передавач, а також приймач і демодулятор ідеальні, тобто сигнал на вході узгодженого фільтра дорівнює сигналу на виході формує фільтра (нижче буде зрозуміло навіщо позначили інший буквою) плюс адитивний білий гаусів шум (AWGN). Тоді загальна частотна характеристика дорівнює добутку. Для виключення МСІ необхідно щоб задовольняла (8). При цьому можна помітити, що повинен бути узгоджений з вихідним сигналом на виході формує фільтра, що означає, що (комплексно-сполучена з формує фільтром). Тоді можна сказати, що, а.
Давайте розбиратися. При використанні узгодженого фільтра для декодування, його частотна характеристика повинна бути комплексно-сполученої частотній характеристиці формує фільтра. Тоді якщо частотна характеристика формує фільтра буде являти собою корінь з піднесеного косинуса, то каскад з формуючого та узгодженого фільтра буде давати саме фільтр Найквіста, який дозволить усунути МСІ при декодуванні.
На малюнку 13 показана імпульсна характеристика і АЧХ фільтра «піднесеного косинуса», (червоний) і фільтра «корінь з піднесеного косинуса» (синій) при. Також показані АЧХ даних фільтрів і в залежності від нормованої частоти.
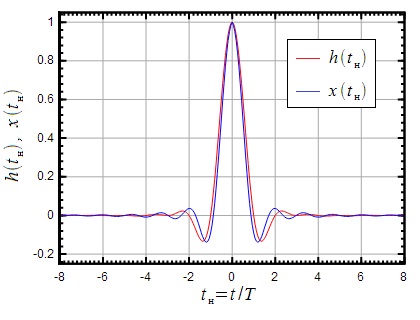
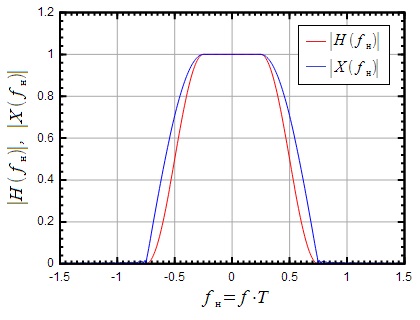
Малюнок 13: Імпульсна характеристика і АЧХ фільтра корінь з піднесеного косинуса
Можна помітити, що фільтр «корінь з піднесеного косинуса» не задовольняє умові відсутності МСІ (дивись рисунок 6), однак якщо поставити послідовно два таких фільтра, то МСІ усувається.
Використання формує фільтра Найквіста для BPSK сигналу
На малюнку 14 наведена структурна схема BPSK модулятора з використанням формує фільтра Найквіста.
Малюнок 14: BPSK модулятор з використанням фільтра Найквіста
Пояснюють осцилограми показані на малюнку 15.
Малюнок 15: Пояснюють осцилограми BPSK модулятора
На верхньому графіку показаний вихідний потік бітів у вигляді біполярних імпульсів, що відповідають інформації, що передається зі швидкістю. Тактовий генератор формує дельта-імпульси з періодом, але зрушені щодо фронтів на полсімвола. Таким чином тактовий генератор управляє ключем, який вибирає з вихідного сигналу значення біт переданої інформації з періодом як це показано на третьому графіку сірими стрілками. Синім показаний сигнал на виході формує фільтра Найквіста з імпульсною характеристикою. Сигнал множиться на несе коливання і виходить на виході BPSK сигнал з обмеженою смугою, отриманий з використанням фільтра Найквіста. В результаті використання фільтра Найквіста в BPSK сигналі змінюється амплітуда під час зміни інформаційних символів.
На малюнку 16 показані осцилограми BPSK сигналу при різних параметрах фільтра Найквіста: (верхній графік) і, фільтр піднесеного косинуса (нижній графік). Швидкість передачі даних при цьому дорівнювала 10 кГц і несуча частота 200 кГц.
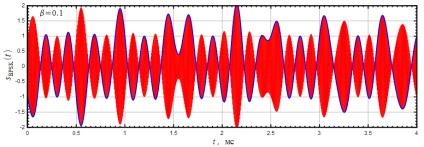
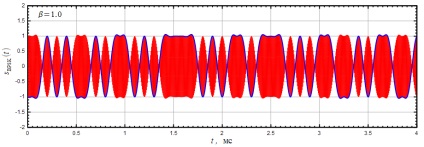
Малюнок 16: Осцилограми BPSK сигналу при різному параметрі фільтра Найквіста
Видно, що при амплітуда сигналу змінюється в менших межах, ніж при. Це також можна проілюструвати Глазкова діаграмами сигналу при різних параметрах, показаних на малюнках 17-19.
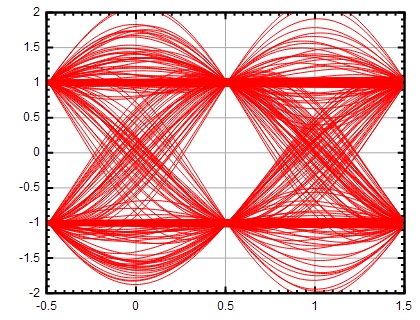
Малюнок 17: Глазкова діаграма при
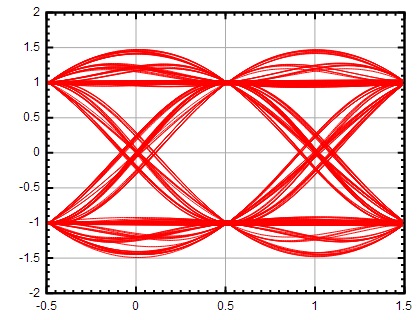
Малюнок 18: Глазкова діаграма при
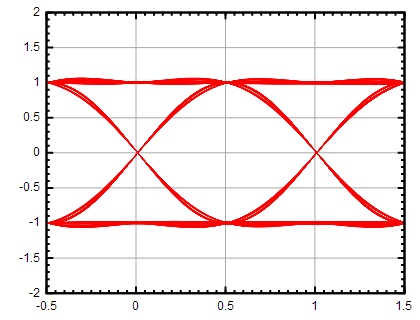
Малюнок 19: Глазкова діаграма при
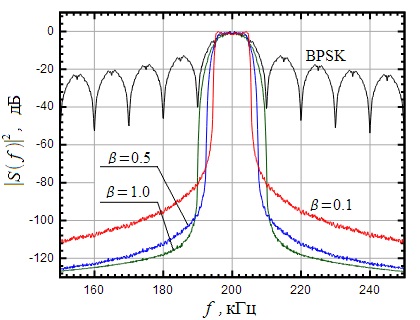
Малюнок 20: Спектр BPSK сигналу при різних параметрах формує фільтра
На малюнку 20 показаний спектр BPSK сигналу при обмеженні смуги за допомогою фільтра Найквіста при різних параметрах, а також спектр BPSK сигналу без використання формує фільтра (чорний графік). Можна помітити, що при обмеженні спектра BPSK сигналу фільтром Найквиста бічні пелюстки повністю придушуються. При цьому ширина спектра при приблизно дорівнює ширині головної пелюстки спектру BPSK сигналу без фільтра Найквіста, т. Е. При маємо швидкість передачі 0.5 біт / c на 1 Гц смуги, а при майже теоретичну межу: 1 біт / c на 1 Гц смуги. При отримуємо проміжне значення ширини смуги сигналу.
Переваги і недоліки використання формує фільтра Найквіста
Головною перевагою використання фільтра Найквіста є можливість звуження смуги сигналу аж до теоретичної межі 1 біт / c на 1 Гц смуги з повним придушенням бічних пелюсток. Однак частіше використовують зі швидкістю передачі 0.5 біт / c на 1 Гц смуги. Це обумовлено головним чином тим, що при отримуємо найбільшу стійкість при передачі даних, крім того амплітудна огинає змінюється в менших межах, а значить, вихідний підсилювач може мати менший динамічний діапазон і більш високий ККД.
Головним недоліком використання фільтра Найквіста при BPSK модуляції є підвищені вимоги до пристрою тимчасової синхронізації при декодуванні інформації, оскільки МСІ відсутня тільки в задані моменти часу відповідні імпульсам тактового генератора. У всі інші моменти часу МСІ дуже велика. Це призводить до меншої завадостійкості сигналу, причому стійкість тим гірше, чим менше параметр і, відповідно, вже смуга.
У даній статті ми ввели поняття межсимвольной інтерференції, що виникає при обмеженні смуги сигналу. Також ми розглянули формує фільтр Найквіста і показали, що теоретичну межу швидкості передачі інформації без МСІ становить 1 біт / c на 1 Гц смуги радіосигналу. Отримано нереалізованим ідеальний формує фільтр, який забезпечує теоретичну межу по швидкості передачі інформації. Також введено фільтр піднесеного косинуса для фізичної реалізованого формує фільтра Найквіста, що дозволяє усунути МСІ. Було показано, що в разі оптимального прийому узгодженим фільтром для усунення МСІ при декодуванні потрібно формує фільтр типу «корінь з піднесеного косинуса». Розглянуто використання фільтра Найквіста для BPSK модуляції з повним придушенням бічних пелюсток спектра.
Будь-які питання і побажання ви можете залишити в гостьовій книзі. на форумі. або надіслати електронною поштою [email protected]