Ця форма (нормальна або напівлогарифмічний) дозволяє представляти в комп'ютері будь-які (цілі, дробові або змішані) числа. Число в формі з плаваючою крапкою записується у вигляді двох частин: мантиси і порядку. Мантиса включає в себе значущі розряди числа, а порядок вказує положення точки. При цьому мантиса запіси-ється як дробове число з фіксованою точкою, а порядок - як ціле число з фіксованою точкою.
Знак мантиси є знаком всього числа, а знак порядку визначає, чи містить число цілу частину.
Значення числа з плаваючою точкою визначається наступним чином:
де т - мантиса числа; q - основа системи числення; р - порядок числа.
Так, в десятковій системі числення число A10 = -123,456 в формі з плаваючою точкою може бути записано таким чином:
При заданих значеннях мантиси і порядку для визначення значення числа потрібно точку (кому) в мантисі перенести на кількість розрядів, рівну величині порядку, вправо для позитивних порядків і вліво для негативних. наприклад:
Число з плаваючою точкою може бути нормалізованим і ненормалізованих. Число не нормалізовано, якщо старша цифра мантиси дорівнює нулю, тобто . Нормалізоване число з плаваючою точкою дозволяє з-зберігати більшу кількість значущих цифр, тому у пам'яті числа зберігаються в нормалізованому вигляді. Нормалізація виконується шляхом зсуву мантиси вліво до тих пір, поки старший розряд мантиси не стане рівним одиниці. Так як значення мантиси при цьому збільшується, для збереження величини числа при зсуві на кожен розряд значення порядку зменшується на одиницю.
Нормалізоване число з плаваючою точкою представляється з точністю, де п - розрядність мантиси. Діапазон чисел з плаваючою точкою становить:
де k - розрядність порядку.
Для збільшення діапазону чисел з плаваючою точкою (за рахунок деякого зменшення точності) двоичная мантиса може розглядатися як шістнадцяткове число. У цьому випадку кожна двоичная тетрада являє одну шестнадцатеричную цифру, тому нормалізація буде порушена лише тоді, коли чотири старших розряду мантиси дорівнюватимуть нулю. Наприклад, якщо старші розряди мантиси мають вигляд 0, 000101. то мантиса вважається нормалізованої, так як тетрада 0001 представляє шестнадцатеричную цифру 1. Поява незначних нулів в мантисі призводить до втрати точності. Разом з тим суттєво збільшується діапазон представлення чисел:
Порядок числа може бути позитивним або отрицатель-ним. Для спрощення операцій над порядками часто використовують зміщений порядок шляхом збільшення дійсного порядку на величину, де k - число розрядів порядку. При цьому зміщений порядок завжди є позитивним числом і тому його знак не вказується. Приклад формату n -розрядним числа з плаваючою точкою і зміщеним порядком представлений на рис. 2.6. Для знака числа відводиться старший розряд, k розрядів займає зміщений порядок, а решта п - k - 1 виділяються під мантиссу. Діапазон і точність представлених у формі з плаваючою крапкою чисел залежать від формату.
Мал. 2.6. Формат числа з плаваючою точкою
Рекомендовані стандартом основні формати чисел з плаваючою точкою представлені на рис. 2.7. Одинарний формат займає 32 розряду, подвійний - 64. Зазвичай для підвищення точності використовують спосіб прихованої одиниці.
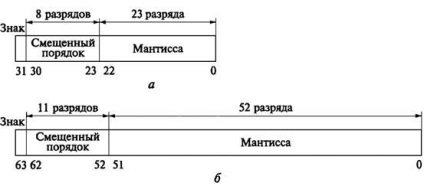
Мал. 2.7. Основні формати чисел з плаваючою точкою:
а - одинарний; б - подвійний
Суть методу полягає в тому, що в нормалізованому числі старший розряд мантиси завжди дорівнює одиниці, тому його можна не записувати, а мати на увазі. Звільнився розряд використовується для запису додаткового розряду мантиси. Перед виконанням арифметичних операцій мається на увазі розряд відновлюється.
В одинарному форматі під зміщений порядок відводиться вісім розрядів, і під мантиссу - 24 (з урахуванням прихованого одиниці). При цьому діапазон представлення чисел становить:. У подвійному форматі зміщений порядок займає 11 розрядів, мантиса - 53, а діапазон представлення чисел складаючи-ет:.
Як і цілі числа, числа з плаваючою точкою можуть бути записані в пакува-ванном форматі. У мікропроцесорах фірми Intel чотири числа одинарної точності (по 32 розряду) упаковуються в групу довжиною 128 розрядів. У таку ж групу упаковуються два числа подвійної-ної точності (по 64 розряду).