Визначення і формула сили Ампера
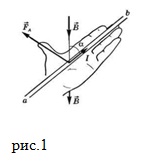
Сила, що діє на провідник зі струмом в магнітному полі, називається силою Ампера. Її позначення:. Сила Ампера векторна величина. Її напрямок визначає правило лівої руки: слід розташувати долоню лівої руки так, щоб силові лінії магнітного поля входили в неї. Витягнуті чотири пальці вказували напрямок сили струму. В такому випадку відігнутий на великий палець вкаже напрям сили Ампера (рис.1).
закон Ампера
Елементарна сила Ампера визначена законом (або формулою) Ампера:
де I - сила струму, - малий елемент довжини провідника - це вектор, який дорівнює за модулем довжині провідника, спрямований в такому ж напрямку як вектор щільності струму, - індукція магнітного поля, в яке поміщений провідник зі струмом.
Інакше цю формулу для сили Ампера записують як:
де - вектор щільності струму, dV - елемент об'єму провідника.
Модуль сили Ампера знаходять відповідно до вираження:
де - кут між векторами магнітної індукції і напрямок течії струму. З виразу (3) очевидно, що сила Ампера максимальна в разі перпендикулярності ліній магнітної індукції поля по відношенню до провідника зі струмом.
Сили, що діють на провідники зі струмом в магнітному полі
Із закону Ампера слід, що на провідник зі струмом, рівним I, діє сила рівна:
де магнітна індукція, що розглядається в межах малого шматочка провідника dl. Інтегрування у формулі (4) проводять по всій довжині провідника (l). З виразу (4) випливає, що на замкнутий контур з струмом I, в однорідному магнітному полі діє сила Ампера дорівнює
Сила Ампера, яка діє на елемент (dl) прямого провідника зі струмом I1. поміщений в магнітне поле, яке створює інший прямий провідник, паралельний першому з струмом I2. дорівнює по модулю:
де d - відстань між провідниками, Гн / м (або Н / А 2) - магнітна постійна. Провідники з струмами одного напрямку притягуються. Якщо напрямки струмів в провідниках різні, то вони відштовхуються. Для розглянутих вище паралельних провідників нескінченної довжини сила Амперана одиницю довжини може бути обчислена за формулою:
Формулу (6) в системі СІ застосовують для отримання кількісного значення магнітної постійної.
Одиниці виміру сили Ампера
Основною одиницею виміру сили Ампер (як і будь-який інший сили) в системі СІ є: [FA] = H
Приклади розв'язання задач
Завдання. Прямий провідник довжини l зі струмом I знаходиться в однорідному магнітному полі B. На провідник діє сила F. Який кут між напрямком течії струму і вектором магнітної індукції?
Рішення. На провідник зі струмом, що знаходиться в магнітному полі діє сила Ампера, модуль якої для прямолінійного провідника зі струмом розташованому в однорідному полі можна уявити як:
де - шуканий кут. отже:
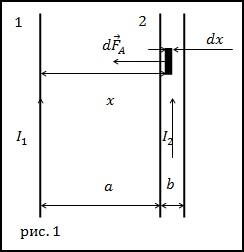
Завдання. Два тонких, довгих провідника зі струмами лежать в одній площині на відстані d одна від одної. Ширина правого провідника дорівнює a. За провідникам течуть струми I1 і I2 (рис.1). Яка, сила Ампера, що діє на провідники в розрахунку на одиницю довжини?
Рішення. За основу рішення задачі приймемо формулу елементарної сили Ампера:
Будемо вважати, що провідник зі струмом I1 створює магнітне поле, а інший провідник в ньому находітся.Станем шукати силу Ампера, що діє на провідник зі струмом I2. Виділимо в провіднику (2) маленький елемент dx (рис.1), який знаходиться на відстані x від першого провідника. Магнітне поле, яке створює провідник 1 (магнітне поле нескінченного прямолінійного провідника зі струмом) в точці знаходження елементаdxпо теоремі про циркуляцію можна знайти як:
Вектор магнітної індукції в точці знаходження елемента dx спрямований перпендикулярно площині малюнка, отже, модуль елементарної сили Ампера, що діє на нього можна уявити як:
де струм, який тече в елементі провідника dx, висловимо як:
Тоді вираз для dFA. враховуючи (2.2) і (2.4) запишемо як:
де з рис.1 видно, що, за умовою задачі силу слід знайти на одиницю довжини, значить. Для знаходження сумарної сили Ампера, що діє на провідник (2) візьмемо подвійний інтеграл від виразу (2.5):
Провідники діють один на одного з силами рівними по модулю і так як струми спрямовані однаково, то вони притягуються.