Якщо підінтегральної функції замінити будь-яким інтерполяційним многочленом, то отримаємо квадратурні формули виду:
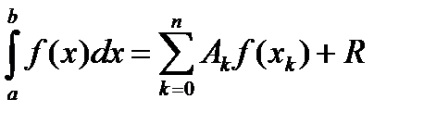
де хк - вибрані вузли інтерполяції; Ak - коефіцієнти, які залежать від обраних вузлів, але не залежать від виду функції f (x); R - залишковий член, який визначає максимальну помилку при використанні квадратурної формули; k = 0, 1, ..., n.
Розбиваючи відрізок інтегрування [a, b] на n рівних частин системою точок
і обчислюючи підінтегральної функції в отриманих вузлах
отримують квадратурні формули для рівновіддалених вузлів. Ці формули називають формулами Ньютона-Котеса. Найбільш зручні при чисельному інтегруванні інтерполяційні многочлени невисоких порядків, при використанні яких отримують досить прості складові формули.
Формула трапецій виходить в разі використання интерполяционного многочлена 1-го порядку:
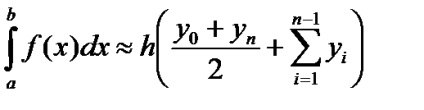
Остаточний член має вигляд: Використання формули трапецій при обчисленні визначеного інтеграла приводить до помилки де
Для знаходження наближеного значення визначеного інтеграла за формулою трапецій можна використовувати алгоритм, схема якого представлена на рис. 5.5.
Помилка обмеження для методу трапецій більше, ніж чим для інших формул Ньютона-Котеса, але його привабливість полягає в простій реалізації. Крім того, незначне ускладнення алгоритму дозволяє істотно знизити похибка обчислень, тому формула трапецій досить часто використовується (в поєднанні з іншими формулами).
Наприклад, в разі апроксимації підінтегральної функції інтерполяційним многочленом Ерміта отримують формулу Ейлера:
Остаточний член цієї формули свідчить про те, що невелика добавка до формули трапецій істотно підвищує її точність.
В останній формулі значення похідних можна замінити двосторонніми різницями
В результаті формула Ейлера перетворюється в формулу Грегорі. але загальний порядок точності знизиться з четвертого до третього.
(2) Формула парабол (Сімпсона)
Використовуючи інтерполяційний многочлен 2-го порядку (параболу) отримують формулу чисельного інтегрування - формулу Сімпсона:
Мал. 5.5 Алгоритм обчислення певного інтеграла за формулою трапецій
На рис. 5.6 показана схема алгоритму, що реалізує обчислення за формулою парабол. При реалізації формули число вузлів обов'язково непарне, т. Е. Число ділянок розбиття інтервалу інтегрування повинно бути парним: n = 2m. В алгоритмі використаний прийом, при якому число повторень циклу зменшується в два рази, т. Е. Двічі реалізується модифікація параметра циклу, що зменшує час виконання алгоритму. Метод Сімпсона вважається одним з найбільш вживаних методів чисельного інтегрування, що забезпечує досить високу точність обчислень.
Мал. 5.6 Алгоритм обчислення певного інтеграла за формулою Сімпсона
(3) Формула Ньютона (правило трьох восьмих)
Більш високу точність обчислення забезпечує інтерполювання підінтегральної функції поліномом третього ступеня. В результаті отримують формулу Ньютона (правило трьох восьмих):
де Схема алгоритму чисельного інтегрування за правилом трьох восьмих показана на рис. 5.7 Практичне застосування знайшли також четверта, п'ята і шоста формули Ньютона-Котеса, проте їх використання призводить до більш громіздким схемами.
Мал. 5.7 Алгоритм обчислення певного інтеграла за формулою Ньютона