Френсіс Хілл "OpenGL. Програмування комп'ютерної графіки. Для професіоналів" стр.224
Опуклі комбінації векторів опуклі комбінації займають важливе місце в математиці і в численних графічних додатках. Опукла комбінація (convex combination) виникає як подальше обмеження аффинной комбінації: не тільки сума коефіцієнтів лінійної комбінації повинна дорівнювати одиниці, але кожен коефіцієнт, крім того, повинен бути невід'ємним. Таким чином, лінійна комбінація з рівності (4.3) є опуклою, якщо
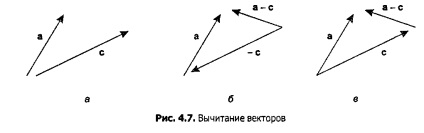
4.2. огляд векторів
Отже, все а<должны находиться между 0 и 1. (Почему?)
Таким чином, 0,3А + 0,7b є опуклою комбінацією векторів а і Ь, в той час як 1,8А - 0,8b - немає. Сукупність коефіцієнтів ava2. am іноді називають розбиттям одиниці (partition of unity), маючи на увазі під цим, що одиничне кількість «матеріалу» розбивається на частини. Опуклі комбінації часто виникають в додатках, де хтось складає одиничне кількість деякої «суміші» і може комбінувати тільки позитивні кількості різних інгредієнтів. Такі комбінації з'являються в найнесподіваніших контекстах. Наприклад, ми побачимо в главі 11, що сплайн-криві фактично є опуклими комбінаціями деяких векторів, а в наших дослідженнях кольору (в главі 12) дізнаємося, що будь-який колір одиничної яскравості можна представити у вигляді випуклої комбінації трьох простих квітів!
Нам видається корисним поняття «множина всіх опуклих комбінацій» деякого набору векторів. Для двох векторів v4 і v2 безліч всіх опуклих комбінацій являє собою безліч всіх векторів виду
де параметр а може змінюватися від 0 до 1. (Чому?) Що це за безліч? Перетворюючи рівність (4.6), отримаємо:
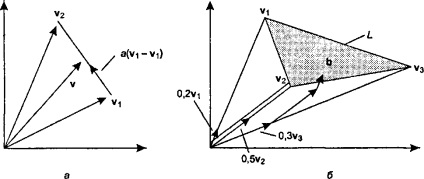
Мал. 4.8. Безліч векторів, які представлені опуклими комбінаціями На рис. 4.8, а показаний вектор v, який дорівнює сумі v, і деякої частини від \ 2 v. причому кінець вектора v розташований на прямій, що з'єднує v, і у2. Так як а змінюється від 0 до 1, кінець v може займати положення, що збігаються з усіма точками відрізка прямої, що з'єднує кінці v, і у2, і тільки ці положення.