В комбінаториці поєднанням з N різних елементів по M називається набір M елементів, вибраних з безлічі N елементів. Такі набори відрізняються тільки входженням в них M певних елементів, порядок проходження елементів в такому наборі не важливий. Набори, що відрізняються тільки порядком проходження елементів (але не складом), вважаються однаковими, і цим поєднання відрізняються від розміщень.
Сполучення без повторень
Завдання. Знайти всі можливі поєднання без повторень з безлічі елементів по 2.
Існують наступні поєднання:
Кількість можливих поєднань без повторень з N елементів по M можна визначити за формулою (N≥M):
що в M! раз менше відповідної кількості розміщень без повторень (оскільки поєднання без повторень не залежить від порядку проходження елементів).
Розглянемо задачу отримання всіх сполучень для чисел 1. N по M.
Реалізація на С ++
#include
using namespace std;
bool NextSet (int * a, int n, int m)
int k = m;
for (int i = k - 1; i> = 0; --i)
if (a [i]
for (int j = i + 1; j
return true;
>
return false;
>
void Print (int * a, int n)
static int num = 1;
cout.width (3);
cout <
int main ()
int n, m, * a;
cout <<"N = " ;
cin >> n;
cout <<"M = " ;
cin >> m;
a = new int [n];
for (int i = 0; i
Print (a, m);
if (n> = m)
while (NextSet (a, n, m))
Print (a, m);
>
cin.get (); cin.get ();
return 0;
>
Сполучення з повтореннями
Поєднаннями з повтореннями називаються набори по M елементів, в яких кожен елемент безлічі N може брати участь кілька разів. При цьому на співвідношення значень M і N пропустити накладається ніяких обмежень, а загальна кількість сполучень з повтореннями становить
Прикладом такого завдання може служити вибір M листівок з N всіма можливими способами.
Для генерації сполучень з повтореннями скористаємося рішенням для генерації розміщень з повтореннями, розглянутим в цій статті.
Реалізація на С ++
#include
using namespace std;
bool NextSet (int * a, int n, int m)
int j = m - 1;
while (a [j] == n j> = 0) j--;
if (j <0) return false;
if (a [j]> = n)
j--;
a [j] ++;
if (j == m - 1) return true;
for (int k = j + 1; k
return true;
>
void Print (int * a, int n)
static int num = 1;
cout.width (3);
cout <
int main ()
int n, m, * a;
cout <<"N = " ;
cin >> n;
cout <<"M = " ;
cin >> m;
int h = n> m. n. m; // розмір масиву а вибирається як max (n, m)
a = new int [h];
for (int i = 0; i
Print (a, m);
while (NextSet (a, n, m))
Print (a, m);
cin.get (); cin.get ();
return 0;
>
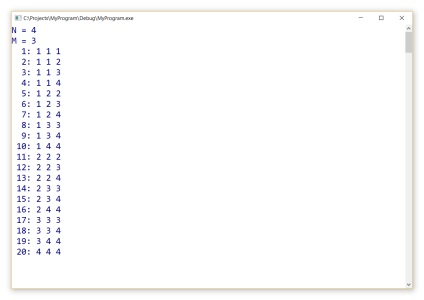
Результат роботи наведеного вище алгоритму: