
Я показав на малюнку, як можна розташувати на шаховій дошці 12 коней (найменше можливе число), щоб при цьому кожна клітина виявилася або зайнятої, або під загрозою нападу коня. Переберія по черзі всі клітини, і ви виявите, що справа йде саме таким чином. Визначте тепер найменше число коней, яке потрібно, щоб кожна клітина виявилася або зайнятої, або під ударом, а кожен кінь був захищений іншим конем. Як випливає розставити цих коней? Можна помітити, що з 12 зображених на малюнку коней лише 4 захищені так само.
Під охороною шахівниця
На звичайній шаховій дошці 8 × 8 кожну клітину можна зробити захищеною (тобто або зайнятої, або атакований) за допомогою п'яти ферзів - найменшого можливого кількості. Існує рівно 91 фундаментально різне розташування, при якому жоден ферзь не атакує іншого ферзя. Якщо кожен ферзь повинен атакувати іншого ферзя (або бути їм захищеним), то існує щонайменше 41 розташування, і я знайшов 150 способів, при яких деякі ферзі атаковані, а деякі ні, але в останньому випадку дуже важко точно перерахувати всі рішення.
На звичайній шаховій дошці кожну клітину можна захистити вісьмома турами (найменше число) 40 320 способами, якщо жодна тура не має права атакувати іншу човен, але не відомо, скільки серед них істотно різних способів (див. Вище рішення задачі "Вісім тур") . Я не перерахував способи, при яких кожна тура захищена інший турою.
На звичайній шаховій дошці кожну клітину можна захистити вісьмома слонами (найменше число), якщо жодному слону забороняється атакувати іншого слона. Якщо кожен слон повинен виявитися захищеним, то необхідно 10 слонів (див. Вище головоломки "Незахищені слони" і "Захищені слони").
На звичайній шаховій дошці кожну клітину можна захистити дванадцятьма кіньми, якщо все коні, крім чотирьох, не захищені. Але якщо кожен кінь повинен виявитися захищеним, то потрібно 14 коней (див. Вище головоломку "Захист коней").
Якщо мати справу з ферзями на дошках n × n, де n менше 8, то представляють інтерес наступні результати:
1 ферзь захищає дошку 2 × 2 одним істотним способом;
1 ферзь захищає дошку 3 × 3 одним істотним способом;
2 ферзя захищають дошку 4 × 4 трьома істотними способами (захищаючи один одного);
3 ферзя захищають дошку 4 × 4 двома істотними способами (не захищені один одного);
3 ферзя захищають дошку 5 × 5 тридцятьма сім'ю істотними способами (захищаючи один одного);
3 ферзя захищають дошку 5 × 5 двома істотними способами (не захищені один одного);
3 ферзя захищають дошку 6 × 6 одним істотним способом (захищаючи один одного);
4 ферзя захищають дошку 6 × 6 сімнадцятьма істотними способами (не захищені один одного);
4 ферзя захищають дошку 7 × 7 п'ятьма істотними способами (захищаючи один одного);
4 ферзя захищають дошку 7 × 7 одним істотним способом (не захищені один одного).
Розташування на шахівниці, які не перебувають під загрозою нападу
Ми знаємо, що і ферзів можна завжди розмістити на квадратної дошці з n 2 клітинами (якщо n> 3), щоб жоден ферзь при цьому не атакував іншого ферзя. Однак загальної формули, що дозволяє знайти число всіх таких розміщень, ще не знайдено; ймовірно, її просто не існує. Відомі такі результати:
при n = 4 існує 1 фундаментальне рішення, а всього 10 рішень;
при n = 5 існує 2 фундаментальних рішення, а всього 10 рішень;
при n = 6 існує 1 фундаментальне рішення, а всього 4 рішення;
при n = 7 існує 6 фундаментальних рішень, а всього 40 рішень;
при n = 8 існує 12 фундаментальних рішень, а всього 92 рішення;
при n = 9 існує 46 фундаментальних рішень;
при n = 10 існує 92 фундаментальних рішення;
при n = 11 існує 341 фундаментальне рішення.
Очевидно, n тур можна розмістити на дошці n × n так, щоб вони не атакували один одного, n! способами, але от скільки серед них істотно різних, мені вдалося дізнатися лише для чотирьох випадків, коли n дорівнює 2, 3, 4 і 5. Відповідями будуть відповідно 1, 2, 7 і 23 (див. головоломку "Чотири леви").
Ми можемо розмістити 2n-2 слонів на дошці n × n двома способами (див. Головоломку "Збори слонів"). Для дощок зі стороною в 2, 3, 4, 5, 6, 7 і 8 клітин існує відповідно 1, 2, 3, 6, 10, 20, 36 фундаментально різних розміщень. У разі непарного n існує 2 1/2 (n-1) таких розміщень, кожне з яких породжує за допомогою поворотів і відображень по 4 інших розміщення, і 2 n-3 -21 / 2 (n-3) розміщення, які породжують по 8 інших розміщень. У разі парного n їх існує 2 1/2 (n-2). кожне за допомогою поворотів і відображень породжує по 4, і 2 n-3 -2 1/2 (n-4). породжують по 8 розміщень.
На дошці і х і ми можемо розмістити ½ (n 2 + 1) коней, які не атакуючих один одного, в разі непарного п одним істотним способом, а коли і парне, то ½n 2 коней вдається розмістити також одним істотним способом. У першому випадку ми всіх коней розміщуємо на клітинах того ж кольору, що і центральна, а в другому випадку ми їх всіх ставимо тільки на чорні або тільки на білі клітини.
Завдання з двома фігурами
На дошці з n 2 клітинами два ферзя, дві тури, два слона або два коня завжди можна розташувати (безвідносно до того, атакують вони один одного чи ні) способами. Наступні формули показують, скількома із способів дві фігури можна розташувати за умови взаємної атаки і без неї.
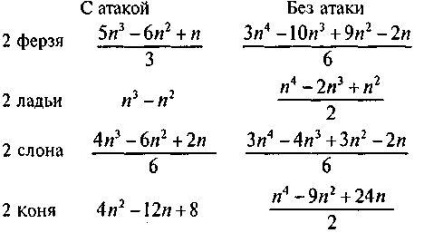
(Див. Головоломку "Полювання на лева".)
Динамічні шахові задачі
147. Турне тури. Єдину туру потрібно пересувати по всій дошці так, щоб вона відвідала кожну клітину рівно по одному разу і закінчила своє турне в тій клітці, з якої його початку. При цьому слід зробити якомога менше число ходів, але якщо ви будете не дуже уважні, то зробите рівно на один хід більше, ніж потрібно. Зрозуміло, клітина вважається "відвідується" як в разі, якщо ви просто проходите через неї, так і в разі зупинки в ній. Нас не повинні хвилювати софізми на кшталт того, що ми двічі відвідуємо вихідний квадрат. Будемо вважати, що ми відвідуємо його один раз.

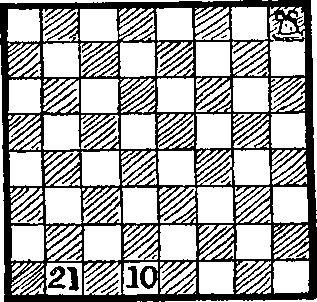
148. Подорож човна. У назві цієї головоломки я не випадково вжив слово "подорож", оскільки слово "турне" означає повернення в вихідне місце, а в даному випадку ми не будемо цього робити. Тура робить 21 хід, відвідавши кожну клітину дошки рівно по одному разу, зупиняється в клітці 10 в кінці десятого ходу і закінчує подорож в клітці 21. Два послідовних ходу не можна робити в одному і тому ж напрямку; іншими словами, ви повинні повертати після кожного ходу.
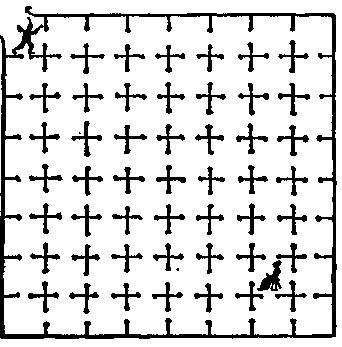
149. Ще одна нудиться діва. Злий барон в добрі старі часи заточив одну безневинну дівчину в глибоку темницю, яка перебувала під ровом замку. На малюнку ви бачите 63 камери в'язниці, які з'єднані між собою відкритими дверима, і камеру, де прикута діва. Якийсь доблесний лицар, який любив цю дівчину, зумів визволити її з рук ворога. Добравшись до входу в темницю, як показано на малюнку, він потім дійшов і до камери, де нудилися діва, відвідавши по дорозі кожну камеру рівно по одному разу. Візьміть олівець і спробуйте позначити його шлях. Досягнувши успіху в цьому, спробуйте звести цей шлях до 22 прямолінійним відрізках. Це можна зробити, як і раніше не відвідавши жодну камеру двічі.
150. Підземелля. Сталося колись у Франції, що один в'язень за власні чи гріхи або гріхи чужі був кинутий в підземеллі, де налічувалося 64 камери, пов'язані між собою відкритими дверима, як показано на малюнку. Щоб чимось скрасити одноманітність ув'язнення, він придумував собі різні головоломки. Ось одна з них.