геодезичний купол (будинок та інші споруди)

Давно відвідували мене думки про будівництво власного будинку, але якось у вигляді цікавих ідей, які помічав у інших в житті або ЗМІ. Представив тут, як виглядав би будинок, що втілює всі ці ідеї - лисяча нора (землянка), що переходить в дзеркальну сферу, що висить на дереві: D. Загалом, ідейний трансформер що зовні що всередині.
Зараз захопився геодезичними куполами і технологіями застосування цих принципів для будівництва житлових будинків та інших корисних і виробничих споруд (наприклад, навісів, лазень, теплиць, сараїв, цехів, майстерень, ангарів).
А зараз натрапив на цікаву інформацію по ним, зарився, і вирішив писати статтю на майбутнє ... своєрідну шпаргалку, щоб швидко можна було згадати і знайти. Так що в міру надходження інформації буду статтю доповнювати. Упевнений і читачам сайту буде корисно.
Ось такі вони бувають:


















Коротенько про історію і що значить "геодезичний".
Як завжди все нове - це добре забуте старе.
Гео - наш земну кулю Земля
Залишок на Д ... - ділити (стародавні греки ділили і вимірювали її ... і не тільки вони)
Так що, якщо не вдаватися в просторову і діфферінціальной геометрію викривлених просторів))), то геодезичний купол - це купол з частини сфери, вірніше сферичного багатогранника, так як вимірюють землю по точках, на її поверхні, які в нашому випадку є вершинами цього багатогранника . Важливою особливістю є оптимально-розподілене розташування вершин і граней прагнуть до ідеальної сфері. Будується зазвичай на основі ікосаедра (20 трикутних граней) або додекаедру (12 п'ятикутних граней).
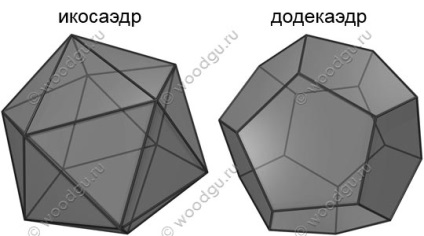
малюнки з блогу: tiaurus.ru (трохи про Піфагора і "магічних фігурах". ікосаедр - стихія води, а додекаедр - всесвіт)
Найбільшого поширення набули геодезичні будинки і споруди на основі ікосаедра. Просував цю справу Річард Бакмінстер Фуллер (американський архітектор, інженер, дизайнер і винахідник). Пишуть, що щільно почав цим займатися з 1947 року. У 1967 році відкрили павільйон США на Всесвітній виставці в Монреалі (на фото нижче). Зараз там начебто музей "біосфера Фуллера".

З наших до цієї теми приклалися М.С. Туполєв, Г.Н. Павлов.
Взагалі, крім геодезичних, видів куполів дуже багато.
ХАРАКТИРИСТИКИ геокупола зазвичай служать:
- частота розбиття межі вихідного багатогранника купола при апроксимації до сфери (позначається літерою V)
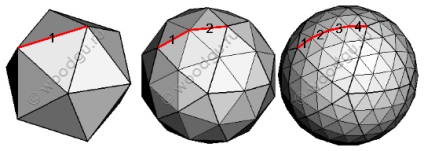
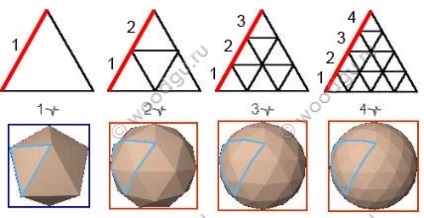
- і частка сфери, яка утворює купол
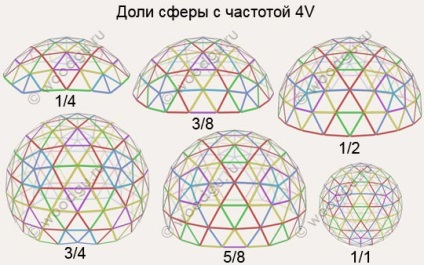
Як видно куполи з високою частотою розбиття мають більш сферичну форму і більшу кількість деталей, відповідно більшу кількість з'єднань. Також видно що точні півсфери 1/2 є у геокуполов з парних розбиттям 2v, 4v, 6v ...
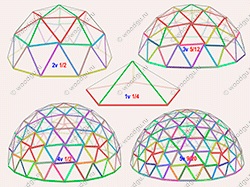
Грані різного кольору позначають межі, різних розмірів.
Кожен рівень призводить до істотного збільшення кількості запилів або конекторів, тобто кожна нова вершина - це плюс від 10 до 24 складних в двох площинах запилів під різними непрямими кутами (при безконнекторной технології) або плюс 10-12 простих відрізів дошки в розмір під прямим кутом і один коннектор (при використанні конекторів).
Наведу наочний приклад, як збільшується обсяг робіт при збільшенні складності купола.
Возмем купол 10 метрів в діаметрі і прорахуємо його в 5 варіантах, як на малюнку вище.
При використанні дошки перетином 200 * 50 мм вийдуть:
1v - 1/4 (частки: 3/4; h = 2,76 м; вершин = 6 шт; l max = 5,276 м; дощок = 10 шт; дерева = 0,51 м 3; S = 47,55 м 2 ) тут половини сфери немає ... є циліндр з одного ряду трикутників в 1/2 сфери і дві кришки як на малюнку ... простіше класичну «коробку» побудувати;
2v -1/2 (частки: 1/4, 3/4; h = 5 м; вершин = 26 шт; l max = 3,093 м; дощок = 65 шт; дерева = 1,84 м 3; S = 73,47 м 2) - трикутники із триметрових дощок треба б все одно зміцнювати перемичками, та й матеріал для обшивки важкувато знайти таких габаритів. хоча якщо використовувати ЛВЛ-брус, то все можливо;
3v - 5/12 (частки: 1/4, 7/12, 3/4; h = 4,14 м; вершин = 46 шт; l max = 2,064 м; дощок = 120 шт; дерева = 2,28 м 3 ; S = 73,87 м 2) - цілком робочий варіант, тільки робити краще 7/12 або спідницю додати;
4v -1/2 (частки: 1/4, 3/8, 5/8, 3/4; h = 5 м; вершин = 91 шт; l max = 1,625 м; дощок = 250 шт; дерева = 3,59 м 3; S = 77,25 м 2) для такого розміру купола один з оптимальних. при діаметрі купола 8,9 м трикутники обшивки майже без залишку кроять з листа OSB шириною 1,25 м
5v - 9/20 (частки: 1/4, 7/20, 11/20, 13/20, 3/4; h = 4,48 м; вершин = 126 шт; l max = 1,308 м; дощок = 350 шт ; дерева = 3,99 м 3; S = 76,81 м 2) - вже перебір і з матеріалами і кількістю робіт
Пояснення до прикладу:
частки - можливе розподіл сфери, крім розрахункового (зліва) і 1/1
h - висота купола;
вершин - кількість вершин многогранника = кількість конекторів, якщо вони є;
l max - довжина найдовшої дошки;
дощок - кількість дощок для каркаса купола;
дерева - кількість дерева в м 3 необхідне для побудови каркасу;
S - площа підстави.
дані отримані за допомогою калькулятора для геодезичних куполовacidome.ru
Продовження на наступній сторінці.
1 nbsp2 nbsp3 nbsp