У цій статті ми постараємося описати що таке геодезичний купол простими словами. По суті - геодезичний купол - це сітка, побудована з безлічі "граней" (багатогранників), максимально близька до форми сфери.
Якщо придивитися, то саме трикутники стали основою сітки, а не ромби, квадрати або шестигранники. Трикутник був обраний як найстабільніша і міцна геометрична структура з усіх відомих. І тому, структура з трикутників (в нашому випадку геокупол), дуже міцна і має самонесущими здібностями. Вона "тримає" сама себе, будучи цілісною структурою. Чим більше граней ми використовуємо для побудови, тим міцніше наша сітка, і більш згладжена форма.
Розглянувши геодезичний купол уважно, стає помітно, що структура побудови геодезичної сітки не є хаотичною, а являє собою строгу математичну модель. Ця модель бере свій початок з геометрії Платонових тіл, правильних багатогранників, відкритих вченими ще в далекому минулому.
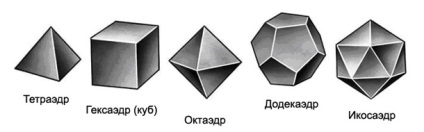
В основі побудови геодезичного купола лежать Платонова Тіла, всього яких налічується п'ять, але ми розглянемо детально тільки Ікосаедр, як найбільш поширений варіант. Ікосаедр - це правильний багатогранник, що складається з 30 однакових ребер, які створюють 20 рівносторонніх трикутників.
Отже, розглянемо побудову геодезичного купола поетапно:
1. Для початку ми будуємо сферу з заданим радіусом

2. Далі ми будуємо ікосаедр "вписаний" в сферу. В цьому випадку всі 12 вершин ікосаедра лежать на поверхні сфери. Всі трикутники рівні.

3. Оскільки всі трикутники в Ікосаедр рівні, ми вибираємо будь-який з них і розбиваємо його на більш дрібні равносторонние трикутники. У нашому випадку розбивка відбувається в п'ятій частоті (про це піде мова пізніше). Обраний початковий трикутник ікосаедра ділитися на 5 "рядів" дрібніших трикутників. Так виходить наша "плоска" розбивка сітки.

4. На цьому етапі ми будуємо відрізки виходять з центру сфери. Ці відрізки повинні проходити через точки з'єднання вийшла сітки і закінчуватися на поверхні сфери.
5. Далі ми з'єднуємо все вершини відрізків, що лежать тепер на поверхні сфери. У нас вийшла структура з трикутників, вершини яких лежать на поверхні сфери, практично повторюючи її форму. Оскільки всі початкові трикутники ікосаедра однакові, то ми можемо сміливо копіювати нашу вийшла сітку, отримуючи бажаний геодезичний купол або сферу.

Частота тріангуляції геодезичного купола
Поняття "частота" або "частота тріангуляції" часто зустрічається в розрахунках геокупола. Вона має на увазі щільність розбивки купола на трикутники. Тобто один і той же купол можна "описати" різною кількістю трикутників. Наприклад, для меншої щільності розбивки потрібно менше трикутників, але з більшою довжиною ребра і форма буде більш незграбною. Для більш щільної розбивки потрібно більшу кількість трикутників з меншою довжиною ребра, але форма вийде більш рівною і близькою до сферичної.
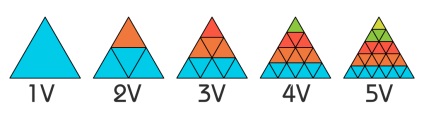
У світі використовується стандартне позначення частоти латинської буквою "V". Нижче наведені приклади тріангуляції до п'ятого значення. Як Ви помітите, число значення частоти дорівнює кількості "рядів", на які ділитися один з трикутників ікосаедра.
Яку частоту вибрати Вам для свого геодезичного купола - вирішувати Вам. Цей параметр залежить від багатьох параметрів: розмірів купола, несучих та інших характеристик матеріалів, довжини ребер, економічності і естетики.
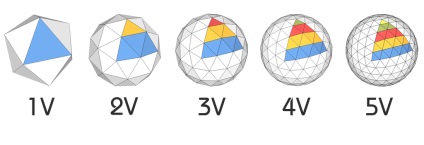
перетин сфери
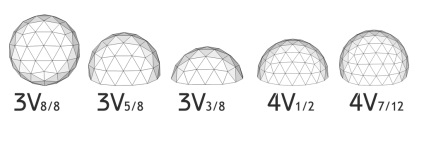
Наступний параметр, який слід знати всім при розрахунку геодезичного купола - це значення перетину сфери. Якщо ми розглянемо сферу як ціле, ми можемо поділити її на різну кількість частин. Оскільки геодезична "розбивка" складається з "рядів", то розбити купола найзручніше за цими рядах. У куполів з різною частотою "V" - різну кількість "рядів", тому перетин для них завжди індивідуальне. Нижче наведені деякі приклади перетину куполів різної частоти.
Ви можете подивитися і вивчити способи побудови геодезичних куполів, заснованих на інших платонових тілах (октаедр, куб і т.д.) за цим посиланням