геометричні паркети
Паркет (або мозаїка) - нескінченне сімейство багатокутників, що покриває площину без просвітів і подвійних покриттів. Іноді паркетом називають покриття площині правильними багатокутниками, при якому два багатокутника мають або загальну сторону, або загальну вершину, або зовсім не мають спільних точок; але ми будемо розглядати як правильні, так і неправильні багатокутники. Отже, якими ж багатокутниками можна замостити площину?
Паркети з однакових правильних багатокутників
Сума всіх кутів n-кутника дорівнює 180 ° (n-2). Всі кути правильного багатокутника рівні; отже, кожен з них дорівнює 180 ° (n-2) / n. У кожній вершині паркету сходиться ціле число кутів; тому число 2 · 180 ° має бути цілим кратним числа 180 ° (n-2) / n. Перетворимо відношення цих чисел:
Різниця n-2 може приймати лише значення 1, 2 або 4; тому n може дорівнювати лише 3, 4 або 6. Значить, можна отримати паркети, складені з правильних трикутників, квадратів або правильних шестикутників.
Паркети з різних правильних багатокутників
Спочатку з'ясуємо, скільки різних правильних багатокутників (з однаковими довжинами сторін) може перебувати навколо кожної точки. Величина кута правильного багатокутника повинна знаходитися в інтервалі від 60 ° до 180 ° (не включаючи); отже, число багатокутників, що знаходяться в околиці точки, має бути більше 2 (360 ° / 180 °) і не може перевищувати 6 (360 ° / 60 °).
Можна показати, що існують такі способи укласти паркет комбінаціями правильних багатокутників: (3,12,12); (4,6,12); (6,6,6); (3,3,6,6) - два варіанти паркету; (3,4,4,6) - чотири варіанти; (3,3,3,4,4) - чотири варіанти; (3,3,3,3,6); (3,3,3,3,3,3) (цифри в дужках - позначення багатокутників, що сходяться в кожній вершині: 3 - правильний трикутник, 4 - квадрат, 6 - правильний шестикутник, 12 - правильний двенадцатіугольнік). Деякі варіанти паркету показані на малюнках:
Паркети з неправильних багатокутників
Легко покрити площину паралелограма:
Взагалі можна замостити площину копіями довільного чотирикутника, необов'язково опуклого:


Можна скласти паркет з копій довільного трикутника: з двох рівних трикутників можна скласти паралелограм, і покрити площину копіями цього паралелограма.
Ще площину можна покрити копіями центрально-симетричного шестикутника, або копіями п'ятикутника з двома паралельними сторонами. До сих пір не знайдені всі типи опуклих п'ятикутників, з яких складаються паркети. Зате доведено теорему, яка стверджує: «Не можна скласти паркет з копій опуклого семикутника». У той же час існують паркети з неопуклих семикутник:
Паркети з довільних фігур
Деякі визначення паркету не обмежуються багатокутниками; в цьому випадку паркетом називається покриття площині без пропусків і перекриттів заданими фігурами (в окремому випадку - багатокутниками, правильними чи неправильними, опуклими або неопуклого). У такому випадку навіть для паркету з багатокутників може не дотримуватися вимога "два багатокутника повинні мати загальну вершину, загальну сторону або зовсім не мати спільних точок"; крім того, з'являється безліч різноманітних паркетів, що складаються не з багатокутників, а з криволінійних фігур. Розглянемо способи побудови нового паркету, виходячи з цього "розширеного" визначення. Отже, як намалювати паркет? (Деякі з можливих способів)
Спосіб перший. Беремо деяку сітку (вже відомий нам паркет) - з правильних трикутників, шестикутників, квадратів, або з довільних багатокутників, і виконуємо перетворення: стиснення / розтягування, заміна прямолінійних відрізків кривими з початком і кінцем в тих же точках, що і у відрізків.
Приклад: паркети, отримані заміною відрізків "квадратної" сітки деякими кривими або ламаними.
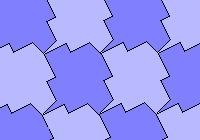
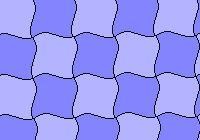

Спосіб другий. Об'єднуємо окремі елементи вже існуючих паркету. Приклади: паркети, отримані в результаті об'єднання елементів квадратної сітки:



Паркет, кожен елемент якого отримано в результаті об'єднання п'яти правильних трикутників:

Спосіб третій. Беремо існуючу сітку і доповнюємо її новими лініями. Отримуємо розбиття площині на фігури, які потім можна по-новому об'єднати. В окремому випадку - накладаємо один на одного дві (або більше) сітки вже відомих паркету, зміщуючи або повертаючи одну сітку щодо іншої; фігури, що утворилися при перетині ліній, вважаємо елементами паркету.
Приклад (розбиття сітки з грецьких хрестів):
Спосіб четвертий. Вибираємо деяку криву або ламану і починаємо її переносити на деякий вектор, наприклад, повертати,. отримані криві або ламані розміщуємо на площині таким чином, щоб вони утворили замкнуті контури (які в подальшому будуть розглядатися як елементи паркету). Якщо розглядати тільки незамкнуті криві і ламані, паркети будуть нагадувати отримані способом №1.
Для отримання наступного паркету була взята дуга спіралі, три рази повернута на 90 °, а потім до отриманої фігурі був застосований паралельний перенос.
А ось паркети, отримані за допомогою паралельного перенесення зірчастих многокутників:


Поєднуючи вершини зірчастих многокутників, отримуємо паркети, що складаються з правильних восьмиугольников, рівнобедрених прямокутних трикутників, а також з неопуклих 16-кутників, що нагадують хрест. На першому малюнку є ще один елемент - опуклий чотирикутник.
Також при підготовці сторінки були використані матеріали, підготовлені мною для УМК "Геометричні паркети" ( "Як намалювати паркет, або чому не буває зошитів в кружечок").
Див. Також: Одинадцять правильних паркету на сайті Кавун