У геометрії є безліч завдань, в яких потрібно знайти найбільше або найменше значення функції. В якості опції можуть розглядатися периметр або площа фігури або, наприклад, обсяг тіла, а аргументом функції служить будь-якої параметр фігури або тіла - довжина сторони, кут між сторонами і т.п. Після того, як функція складена, її необхідно досліджувати за допомогою похідної на екстремальне значення. При цьому слід враховувати, що зазвичай в таких прикладах функція існує на кінцевому проміжку, який визначається геометрією системи і умовою завдання.
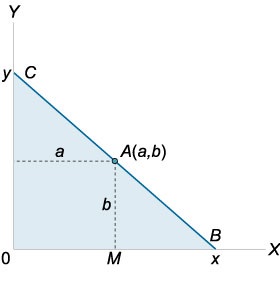
На координатної площини в першій чверті задана точка \ (A \ left (\ right). \) Провести через цю точку пряму, що відсікає трикутник найменшої площі, обмежений даної прямий і осями координат (рисунок \ (1 \)).
Розглянемо трикутники \ (OBC \) і \ (MBA. \) Ці трикутники подібні. Отже, справедливо співвідношення \ [\ frac >> = \ frac >> \; \; \ text \; \; \ frac = \ frac>, \] де координати \ (x \) і \ (y \) задовольняють співвідношенням \ (x> a, \) \ (y> b. \) звідси висловимо \ (y \) через \ (x: \) \ [y = \ frac >>. \] Площа трикутника буде описуватися наступній функцією \ (S \ left (x \ right): \) \ [> = \ frac \ cdot \ frac >>> = >> \ right) >>.> \] Обчислимо похідну: \ [>> \ right) >>> \ right) ^ \ prime >> = >>>> \ right) ^ \ prime >> = \ cdot \ frac \ right) - >> \ right)> ^ 2 >>>> = \ cdot \ frac - 2ax - >> \ right)> ^ 2 >>>> = \ right) >> \ right)> ^ 2 >>>.> \] Функція \ (S \ left (x \ right) \) має критичні точки \ (x = 0, \) \ (x = a, \) \ (x = 2. \) Оскільки \ (x> a, \) то рішенням є точка \ (x = 2a. \) При переході через неї похідна змінює знак з хв са на плюс, тобто \ (X = 2a \) - точка мінімуму функції \ (S \ left (x \ right). \)
Обчислимо інший катет трикутника: \ [\ require y = \ frac >> = \ frac >> = \ frac> = 2b. \] Таким чином, трикутник з найменшою площею має катети, рівні \ (2a \) і \ (2b. \)
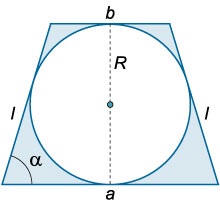
Рівнобедрена трапеція описана навколо кола радіуса \ (R \) (рисунок \ (2 \)). При якому куті при підставі \ (\ alpha \) площа заштрихованої області буде найменшою?
Площа рівнобедреної трапеції визначається формулою \ [= \ frac> \ cdot h, \] де \ (a, b \) - підстави трапеції, \ (h \) - її висота. Очевидно, що \ (h = 2R. \) Площа кола дорівнює \ (= \ pi. \) Тоді площа заштрихованої області становить \ [- = \ frac> \ cdot 2R - \ pi> = \ right) R - \ pi. > \] Оскільки трапеція описана навколо кола, то сума протилежних сторін у неї однакова, тобто \ [\; \; >>>> = >>.> \] Тут через \ (\ ell \) позначена бічна сторона трапеції. Підставляючи \ (\ left (\ right) \) в попереднє співвідношення, отримуємо: \ [>> \ cdot R - \ pi> = \ left (> - \ pi> \ right).> \] Досліджуємо площа \ (S \ left (\ alpha \ right) \) на екстремальне значення. Обчислимо похідну \ (S '\ left (\ alpha \ right): \) \ [\ left (> - \ pi> \ right)> \ right] ^ \ prime >> = \ left ( <- \frac^2>\ Alpha >>> \ right) \ cdot \ cos \ alpha> = <- \frac\cos \alpha>> ^ 2> \ alpha >>.> \] Видно, що похідна дорівнює нулю за умови \ [\ cos \ alpha = 0, \; \; \ Rightarrow \ alpha = \ frac, \] причому при переході через цю точку (при зростанні \ (\ alpha \)) похідна змінює знак з мінуса на плюс. Отже, \ (\ alpha = \ large \ frac \ normalsize \) - точка мінімуму функції \ (S \ left (\ alpha \ right). \) У цьому випадку трапеція "вироджується" в квадрат. Мінімальне значення площі фігури визначається формулою \ [> = \ left (\ right). \]
Вікно має форму прямокутника, обмеженого зверху півколом (рисунок \ (3 \)). Периметр вікна дорівнює \ (P. \) Визначити радіус півкола \ (R, \) при якому площа вікна є найбільшою.
Очевидно, що одна сторона прямокутника дорівнює \ (2R. \) Іншу сторону позначимо через \ (y. \) Периметр всього вікна виражається формулою \ [P = \ pi R + 2R + 2y. \] Звідси знаходимо \ (y: \) \ [y = \ frac \ left [\ Right]. \] Площа вікна становить: \ [>> + 2Ry> = >> + 2R \ cdot \ frac \ left [
\ Right]> = >> + PR - \ pi - 2> = >> - 2.> \] Отриманий вираз являє собою функцію \ (S \ left (R \ right). \) Досліджуємо її на екстремум. Знаходимо похідну: \ [>> - 2> \ right) ^ \ prime >> =
=
\] Визначаємо стаціонарні точки: \ [\; \; \ Right) R = 0,> \; \;>.> \] Оскільки друга похідна негативна: \ [\ right) R> \ right] ^ \ prime >> = <- \left( \right) r\)). Из данного бревна требуется вырезать балку в форме параллелепипеда с квадратным сечением наибольшего объема.
Будемо вважати, що осі колоди і балки збігаються. Усічений конус і вписаний в нього паралелепіпед схематично показані в розрізі на малюнку \ (14. \) Обсяг паралелепіпеда визначається формулою \ [V = y, \] де \ (x \) - сторона квадрата в основі паралелепіпеда, а \ (y \) - його висота.