Записи з міткою "геометричний зміст похідної"
Виведемо рівняння дотичної до графіка функції y = f (x) в точці з абсцисою х0. Для наочності використовуємо графік з
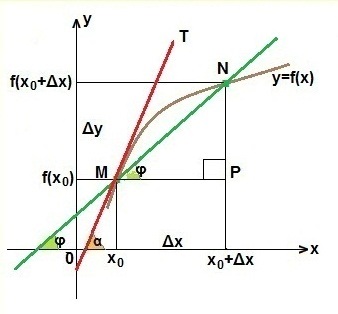
Так як точку М ми взяли довільно, то повинні отримати рівняння дотичній, яке буде справедливо для будь-якої функції y = f (x). має дотичну в певній точці з абсцисою х0.
Отже, будь-яку пряму можна записати у вигляді y = kx + b. де k - кутовий коефіцієнт прямої. Ми тепер знаємо, що в якості кутового коефіцієнта можна взяти f '(х0) - значення похідної функції y = f (x) в точці з абсцисою х0. Ця точка є спільною точкою для функції і для дотичній МТ.
Таким чином, дотична МТ має вигляд: y = f '(х0) · x + b. Залишилося визначити значення b. Це ми зробимо просто: підставимо координати точки М в останню рівність, тобто замість х запишемо х0. а замість у підставимо f (х0). Отримуємо рівність:
Виконати наступні завдання.
1. Написати рівняння дотичної до графіка функції y = x 2 в точці x0 = 3. Зробити креслення.
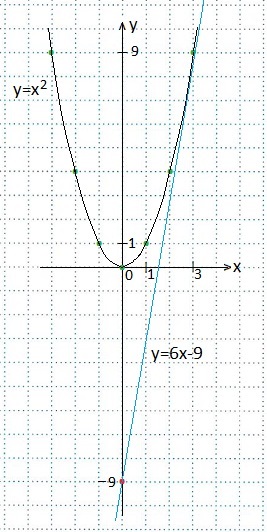
Знаходимо значення даної функції в точці з даної абсциссой:
Знаходимо похідну f '(x) = (x 2)' = 2x і знаходимо значення цієї похідної при х = 3.
Підставами знайдені значення
y = 6 x-9 - шукане рівняння дотичної.
2. Написати рівняння дотичної до графіка функції
Записуємо загальне рівняння дотичній: y = f (x0) + f '(x0) (x-x0). Знаходимо значення даної функції в точці х = 1. отримуємо:
f (x0) = f (1) = 1. Знайдемо похідну даної функції за формулою похідної ступеня:
Знаходимо значення цієї похідної при х = 1.
f '(x0) = f (1) = - 2 · (1) -3 = -2. Підставляємо знайдені значення в загальне рівняння дотичній:
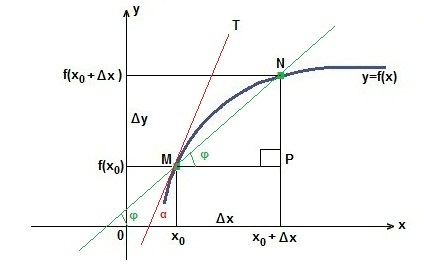
Δy = f (х0 + Δх) - f (x0). Через точки M і N проведемо січну MN. яка утворює кут φ з позитивним напрямком осі Ох. Визначимо тангенс кута φ з прямокутного трикутника MPN.
Нехай Δх прагне до нуля. Тоді січна MN буде прагнути зайняти положення дотичної МТ. а кут φ стане кутом α. Значить, тангенс кута α є граничне значення тангенса кута φ:
Визначення похідної. Границя відношення приросту функції до приросту аргументу, при прагненні останнього до нуля, називають похідною функції в даній точці:
Геометричний зміст похідної полягає в тому, що чисельно похідна функції в даній точці дорівнює тангенсу кута, утвореного дотичною, проведеною через цю точку до даної кривої, і позитивним напрямом осі Ох:
1. Знайти приріст аргументу і приріст функції y = x 2. якщо початкове значення аргументу дорівнювало 4. а нове -4,01.
Нове значення аргументу х = х0 + Δx. Підставами дані: 4,01 = 4 + Δх, звідси приріст аргументу Δх = 4,01-4 = 0,01. Приріст функції, за визначенням, дорівнює різниці між новим і попереднім значеннями функції, тобто Δy = f (х0 + Δх) - f (x0). Так як у нас функція y = x 2. то Δу = (х0 + Δx) 2 - (х0) 2 = (х0) 2 + 2x0 · Δx + (Δx) 2 - (х0) 2 = 2x0 · Δx + (Δx) 2 =
Можна було приріст функції знайти по-іншому: Δy = y (х0 + Δx) -y (х0) = у (4,01) -у (4) = 4,01 2 -4 2 = 16,0801-16 = 0 , 0801.
Значення похідної в точці дотику х0 і є значення тангенса кута нахилу дотичної (геометричний зміст похідної). Маємо: f '(х0) = tgα = 1 → α = 45 °, так як tg45 ° = 1.
Відповідь: дотична до графіка даної функції утворює з позитивним напрямом осі Ох кут, рівний 45 °.
3. Вивести формулу похідної функції y = x n.
Диференціювання - це дія знаходження похідної функції.
При знаходженні похідних застосовують формули, які були виведені на підставі визначення похідної, так само, як ми вивели формулу похідної ступеня: (x n) '= nx n-1.
Таблицю похідних легше буде завчити, промовляючи словесні формулювання:
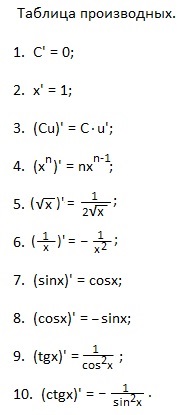
1. Похідна постійної величини дорівнює нулю.
2. Ікс штрих дорівнює одиниці.
3. Постійний множник можна винести за знак похідної.
4. Похідна ступеня дорівнює добутку показника цього ступеня на ступінь з тим же підставою, але показником на одиницю менше.
5. Похідна кореня дорівнює одиниці, поділеній на два таких же кореня.
6. Похідна одиниці, поділеній на ікс дорівнює мінус одиниці, поділеній на ікс в квадраті.
7. Похідна синуса дорівнює косинусу.
8. Похідна косинуса дорівнює мінус синусу.
9. Похідна тангенса дорівнює одиниці, поділеній на квадрат косинуса.
10. Похідна котангенс дорівнює мінус одиниці, поділеній на квадрат синуса.
Вчимо правила диференціювання.
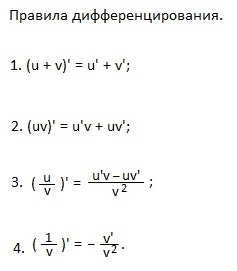
2. Похідна твори дорівнює добутку похідної першого множника на другий плюс твір першого множника на похідну другого.
3. Похідна «у», поділеного на «ве» дорівнює дробу, в чисельнику якого "у штрих помножений на« ве »мінус« у, помножений на ве штрих », а в знаменнику -« ве в квадраті ».
Сторінка 1 з 1 1