Визначення гіперболічної спіралі
Гіперболічна спіраль - плоска трансцендентна крива, рівняння якої в полярних координатах має вигляд:
Крива складається з двох гілок, симетричних відносно прямої (див. Рис.). Початок координат є асимптотической точкою. Асимптота - пряма, паралельна полярної осі і віддалена від неї на відстані.
Гіперболічна спіраль виходить при русі точки по обертається прямий таким чином, що її відстань від центру обертання завжди буде обернено пропорційно куту повороту прямий, виміряного від початкового положення.
I.Найдем площа сектора:
II.Вичіслім довжину дуги гіперболічної спіралі, використовуючи формулу:
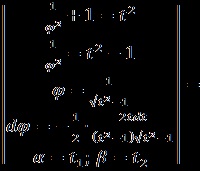
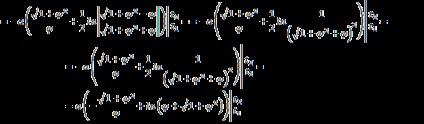
Отже, довжина дуги між точками M1 (,) і M2 (,) має вигляд:
1. Великий енциклопедичний словник «Математика»,
4. Маркушевич А.І. Чудові криві, М. 1978 р
7. Фихтенгольц Г.М. Курс диференціального й інтегрального числення; том I, II- М. Наука, 1969
9. Графіки функцій. Довідник. Вірченко Н.О. Ляшко І.І. Швецов К.І., 1979 г.