Сніжинка має Dih6 діедральную симетрію, ту ж саму, що і правильний шестикутник.
Діедральная група (група діедра) - група симетрії правильного багатокутника. що включає як обертання. так і осьові симетрії [1]. Діедральние групи є найпростішими прикладами кінцевих груп і грають важливу роль в теорії груп. геометрії і хімії. Добре відомо і зовсім тривіально перевіряється, що група, утворена двома інволюція з кінцевим числом елементів в області визначення є діедральной групою.
Позначення [| ]
Є два основних види записи діедральной групи, пов'язаної з n -сторін многоугольником. В геометрії група записується як Dn. в той час як в загальній алгебрі та ж сама група позначається як D2n. використовуючи в якості індексу число елементів в групі. Є також нотація Коксетер. в якій осьова симетрія позначається як [n] (близько 2n), і обертання як [n] + (порядку n). Ще один запис - нотація орбівид. в якій осьова симетрія позначається як * nn. а обертання - як n.
У цій статті Dn (або, іноді, Dihn) відноситься до симетрія правильного n -угольніка.
Визначення [| ]
Елементи [| ]
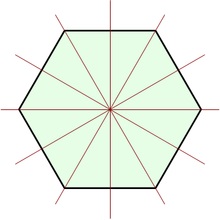
Шість осьових відображень правильного шестикутника
Правильний n -угольнік має 2n різних симетрій: n поворотів і n осьових відображень. утворюють діедральную групу Dn. Якщо n непарне, кожна вісь симетрії проходить через середину однієї зі сторін і протилежну вершину. Якщо n парне, є n / 2 осей симетрії, що з'єднують середини протилежних сторін і n / 2 осей, що з'єднують протилежні вершини. У будь-якому випадку, є n осей симетрії і 2n елементів в групі симетрій. Відображення щодо однієї осі, а потім щодо іншого, призводить до обертання на подвоєний кут між осями. Зображення нижче показують результат дії елемента D8 на дорожній знак Стоп:

Перший рядок показує вісім обертань, а друга - вісім відображень.
Структура групи [| ]
Як і для будь-якого іншого геометричного об'єкта, композиція двох симетрій правильного багатокутника знову буде симетрією. Таким чином, симетрії правильного багатокутника утворюють кінцеву групу.
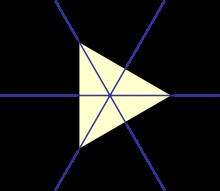
Діедральная група як група симетрії в 2D і група обертань в 3D [| ]
Прикладом абстрактної групи Dihn і загальноприйнятого шляху графічного представленіяt є група Dn ізометрій площині. не рухаються початок координат. Ці групи формують одну з двох серій дискретних груп точок на площині. Dn складається з n обертань на кут, кратний 360 ° / n. навколо початку координат, і відображень щодо n осей, що проходять через центр координат і кутом до решти осях, кратним 180 ° / n. Ці точки представляють групу симетрії правильного багатокутника з n сторонами (для n ≥ 3).
Діедральная група Dn is породжується обертанням r порядку n і відображенням s близько 2, такими що
У термінах геометрії: дзеркальне відображення обертання виглядає як зворотне обертання.
У термінах матриць: задавши
Діедральная група D2 породжується обертанням r на 180 градусів, і симетрією s щодо осі X. Елементи D2 можна уявити як e, r, s, rs>, де e - тотожне перетворення і rs - симетрія відносно осі 'Y.
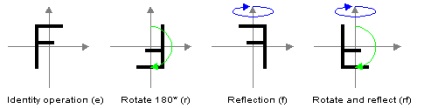
Чотири елементи D2 (тут вісь X вертикальна)
Для n> 2 операції обертання і відображення відносно прямій не комутативні і Dn не є абельовой. Наприклад, в D4. обертання 90 градусів, а потім відображення дає зовсім інший результат, ніж відображення, а потім обертання.
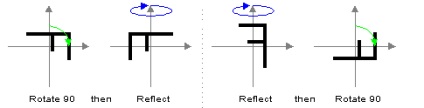
D4 НЕ Абелеві (вісь X тут вертикальна).
Таким чином, поряд з очевидним додатком до проблем симетрії на площині, ці групи служать найпростішими прикладами неабелевих груп, і часто використовуються як контрприклади для теорем, обмежених абелевих груп.
2n елементів Dn можна записати як e. r. r 2, ..., rn -1. s. r s. r 2 s, ..., rn -1 s. Перші n перерахованих елементів є обертаннями, інші n - відображення відносно осей (всі вони мають порядок 2). Результатом двох обертань або двох відображень буде обертання Результат обертання і відображення буде відображенням.
Однак, позначення Dn використовується для підгруп SO (3). які теж являють собою групи типу Dihn. група симетрії багатокутника, вкладеного в тривимірний простір (якщо n ≥ 3). Такі фігури можна розуміти як вироджені тіла (звідси і назва діедрон (dihedron ').
Приклади симетрії двовимірних діедралов [| ]
Еквівалентні визначення [| ]
Наступні визначення Dihn еквівалентні:
- Група автоморфізмів графа складається тільки з циклу з n вершинами (якщо n ≥ 3).
- Група з поданням
Властивості [| ]
Властивості діедральних груп Dihn з n ≥ 3 залежать від парності n. Наприклад, центр групи Dihn складається тільки з тотожності при непарному n. і з двох елементів при парному, а саме, з тотожності і rn / 2
Якщо m ділить n. то Dihn має n / m підгруп виду Dihm. і одну підгрупу Zm. Таким чином, повне число підгруп групи Dihn (n ≥ 1), так само d (n) + σ (n), де d (n) - число натуральних дільників n і σ (n) - сума натуральних дільників n.
Спряженість класів відображень [| ]
Все відображення попарно сполучені в разі непарного n. але розпадаються на два класи спряженості при парному n. У термінах ізоморфізму правильних n -угольніков: для непарних n будь-яку пару відображень можна уявити як обертання, в той час як для парних n тільки половина відображень може бути отримана з деякого обертання поворотами. З геометричної точки зору, в непарному многоугольнике кожна вісь симетрії проходить через одну з вершин і середину протилежної сторони, а в парному є два набори осей, кожен набір відповідає своєму класу пов'язаності - осі, що проходять через вершини і осі, що проходять через середини сторін.
Алгебраїчно, це представники пов'язаних елементів з теореми Силова. для непарних n будь відображення разом з тотожним елементом утворює підгрупу порядку 2, що є сіловской 2-підгрупою (2 = 2 1> - максимальний ступінь двійки, що ділить 2 n = 2 (2 k + 1)), в той час як для парних n . ці підгрупи 2-го порядку не є сіловскую, оскільки 4 (найбільша ступінь двійки) ділить порядок групи.
Для парного n замість цього є зовнішній автоморфизм. переставляти два типи відображень.
Групи автоморфізмів [| ]
Це можна зрозуміти в термінах генератора відображень і елементарних обертань (обертань на k (2 # X03C0; / N). для k взаємно-простого з n). Який автоморфизм буде внутрішнім, а який зовнішнім, залежить від парності n.
- Для непарного n діедральная група не має центру, так що будь-який елемент визначає нетривіальний внутрішній автоморфизм. Для парного n обертання на 180 ° (відображення щодо центру координат) є нетривіальним елементом центру.
- Таким чином, для непарного n. внутрішня група автоморфізмів має порядок 2n, а для парного - порядок n.
- Для непарного n. все відображення є сполученими, для парного, вони розпадаються на два класи (ті, які проходять через дві вершини, і ті, які проходять через середини сторін), і ці два класи пов'язані з зовнішнім автоморфизмом, який можна представити як обертання на # X03C0; / N (половину кута мінімального обертання).
- Обертання дають нормальну підгрупу. Сполучення відображення змінює знак (напрямок) обертання, але в іншому їх не змінюють. Автоморфізм, умножающий кути на k (взамнопростое з n) є зовнішнім, якщо тільки не k = # X00B1; 1.
Приклади автоморфізм груп [| ]
Dih9 має 18 внутрішніх автоморфізмів. Як група ізометрій двовимірного простору, D9 має відображення з інтервалом 20 °. 18 внутрішніх автоморфізмів забезпечують обертання відображень на число, кратне 20 °, і відображення. Як групи ізометрії вони всі є аутоморфізмамі. Є ще, до того ж, 36 зовнішніх автоморфізмів. наприклад, множачи кут обертання на 2.
Узагальнення [| ]
Є кілька важливих узагальнень діедральних груп:
- Нескінченна діедральная група - це нескінченна група з структурою алгебри, схожою на структуру кінцевих діедральних груп. Її можна розглядати як групу симетрій цілих чисел.
- Ортогональна група O (2), тобто група симетрії кола. має властивості, схожі на властивості кінцевих діедральних груп
- Сімейство узагальнених діедральних груп включає вищенаведені розширення, як і багато інших.
- Квазіедральние групи - це сімейство кінцевих груп з властивостями, схожими на властивості кінцевих діедральних груп.
Див. Також [| ]
Примітки [| ]
Посилання [| ]
Для поліпшення цієї статті з математики бажано: