Циліндрична гвинтова лінія 1) являє собою просторову криву лінію однакового ухилу. Вістря різця, стикаючись з поверхнею рівномірно обертового циліндричного стрижня, залишає на ньому слід у вигляді кола. Якщо ж при цьому повідомити різцю рівномірний поступальний рух уздовж осі циліндра, то на поверхні циліндра вийде циліндрична гвинтова лінія.
На рис. 301 показано освіту гвинтовий лінії на поверхні циліндра 2) від руху точки А по котра утворює ЄС і обертального руху цієї утворює. Тут зображено кілька положень цієї утворює: E0 С0. E1, С1. ;
1) Інакше Геліса - від helice (фр.) - спіраль, гвинтова лінія.
2) Таке зображення прямого кругового циліндра розглядалося в курсі креслення середньої школи.
при цьому дуги E0 El. Е1 Е2. рівні між собою і кожна дорівнює - πd / n. де d - діаметр циліндра, а n - число поділок (на рис. 301 n = 12). Початкове положення точки позначено через А0. подальше - відповідно через А1. А2 і т. Д.
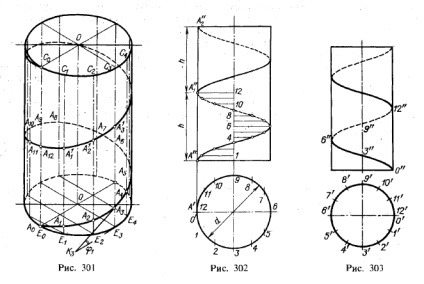
Якщо при переміщенні утворює з положення Е0 С0 в положення Е1 С1 точка займе положення А1 то відрізок Е1 А1 визначить відстань, яке точка пройшла по котра утворює від свого початкового положення. При подальшому положенні утворює (Е2 С2) точка підніметься на висоту Е2 А2 = 2Е1 А1 і т. Д. Коли утворює зробить повний оборот, точка переміститься по ній на відстань E0 Al2 = 12Е1 А1.
При подальшому обертанні утворює точка А почне утворювати другий виток. або оборот гвинтовий лінії. займаючи положення А 1 1. А 1 2 і т. д.
Відстань між точками А0 і А12 називається кроком гвинтової лінії. Крок може бути обраний в залежності від тих чи інших умов.
Відстань точки А до осі 00 називається радіусом гвинтовий лінії. а вісь 00 - віссю гвинтовий лінії. Радіус гвинтовий лінії дорівнює половині діаметра прямого кругового циліндра, на бічній поверхні якого розташовується гвинтова лінія. Дві величини - діаметр циліндра і розмір кроку - є параметрами 1), що визначають циліндричну гвинтову лінію на бічній поверхні прямого кругового циліндра.
На рис. 302 виконано побудову проекцій циліндричної гвинтової лінії. Попередньо побудовані проекції (як це розглядалося в курсі креслення середньої школи) прямого кругового циліндра. Окружність підстави циліндра (на горизонтальній проекції) і крок (відрізок h, відкладений по осі циліндра на фронтальній проекції) розділені на однакове число (n) частин; на рис. 302 взято n = 12. Початкове положення точки А зазначено проекціями А "й А '- це точка, зазначена літерою О' на колі.
1) Параметр (від parametron (грец.) - відмірюють) - величина, числові значення якої дозволяють виділити певний елемент з числа елементів того ж роду.
Так як вісь циліндра спрямована перпендикулярно до пл. π1 то горизонтальна проекція гвинтової лінії зливається з окружністю. представляє собою горизонтальну проекцію поверхні циліндра. Що ж стосується побудови .; фронтальної проекції гвинтової лінії, то хід її побудови ясний з рис. 302 і випливає з самої освіти гвинтовий лінії як траєкторії точки, що здійснює два руху - рівномірний по прямій лінії і разом з тим рівномірний обертальний навколо осі, паралельної цій прямій.
Проекція на площині, паралельної осі циліндра, в даному випадку фронтальна проекція циліндричної гвинтової лінії, подібна синусоїді.
На рис. 302 фронтальна проекція гвинтової лінії має на передній (видимої) стороні циліндра підйом зліва направо або спуск вліво; якщо ж вісь циліндра розташувати горизонтально, то підйом гвинтовий лінії йде вліво, а спуск - вправо. Це гвинтова лінія з правим ходом. або права гвинтова лінія. Гвинтова лінія з лівим ходом (ліва гвинтова лінія) показана на рис. 303 - підйом на фронтальній проекції гвинтової лінії на передній (видимої) стороні циліндра йде
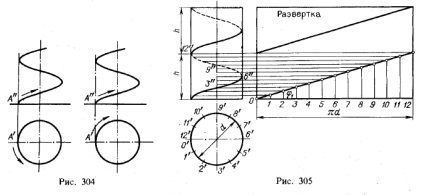
справа наліво, спуск - вправо; якщо ж вісь циліндра розташувати горизонтально, то підйом вправо, а спуск вліво.
Якщо гвинтова лінія зображується без циліндра і без проекцій точок, то вказівка про те, чи є гвинтова лінія правої або лівої, треба давати або написом, або стрілками, так, як це показано на рис. 304 зліва для правої гвинтової лінії, праворуч для лівої 1).
Розгортка витка циліндричної гвинтової лінії показана на рис. 305. У розгорнутому вигляді кожен виток являє собою відрізок прямої. Це випливає з освіти гвинтовий лінії: оскільки окружність підстави циліндра ділилася на рівне число частин і крок гвинтової лінії ділився на таке ж число рівних частин, розгортку гвинтовий лінії на протязі її кроку можна розглядати як геометричне місце точок, для кожної з яких ордината пропорційна абсциссе, т. е. у = KХ. А це рівняння прямої лінії. Дотичні до гвинтової лінії збігаються на розгортці з прямою, в яку розгортається виток гвинтової лінії.
На рис. 305 при двох кроках гвинтовий лінії вийшли два її відрізка під кутом φ1 до прямої, що представляє собою розгорнуту окружність підстави циліндра. Крутизна підйому гвинтової лінії виражається формулою
1) Циліндрична гвинтова лінія добре ілюструється гвинтовий циліндричної пружиною, різьбленням на болтах, гвинтах, шпильках, циліндричним черв'яком.
де h - крок гвинтової лінії, a d - діаметр циліндра. Кут φ1. називається кутом підйому гвинтової лінії.
Довжина одного обороту ( «витка») гвинтовий лінії дорівнює L = √ (h 2 + (πd) 2).
При одному і тому ж d величина кута φ1 залежить тільки від кроку гвинтової лінії; для отримання малого кута підйому слід брати малий крок, і навпаки. Якщо ж крок залишається незмінним для циліндрів різного діаметру, то кут підйому вийде тим менше, чим більше буде діаметр циліндра.
Модель гвинтовий лінії можна побудувати, якщо взяти прямокутник з накресленої на ньому діагоналлю і згорнути його у вигляді прямого кругового циліндра; при цьому діагональ прямокутника утворює один виток гвинтової лінії. Очевидно, що гвинтова лінія є найкоротша відстань між двома точками на поверхні кругового циліндра - геодезична лінія цієї поверхні.
Дійсно, на поверхні такого циліндра між двома точками може бути проведено безліч ліній. Одна з цих ліній дає найкоротша відстань між точками. При розгортанні поверхні така лінія розгортається в пряму. Це притаманне лініях на поверхні, званим геодезичними.
Розглянемо наступне властивість циліндричної гвинтової лінії.
Покладемо (рис. 301), що до гвинтової лінії в який-небудь її точці А3 проведена дотична, яка перетинає пл. π1 в точці К3.
Кут між гвинтовою лінією і будь-який утворює циліндра виражається кутом між цією утворює і дотичній (до гвинтової лінії), проведеної в точці, загальною для гвинтової лінії і утворює. Розгортка на рис. 305 показує, що між даною гвинтовою лінією і утворюють циліндра виходить постійний кут, т. Е. Все дотичні до гвинтової лінії однаково нахилені до створюючих циліндра і перетинають пл. π1 під одним і тим же кутом φ1. Цей же кут був отриманий між розгорненнями гвинтовий лінії і кола основи.
При розгортанні бічній поверхні циліндра з нанесеною на ній гвинтовою лінією, наприклад, елемент А0 А3 Е3 (рис. 301) приймає форму прямокутного трикутника К3 А3 Е3. в якому К3 А3 є дотичною до гвинтової лінії в точці А3. а К3 Е3 - проекцією дотичній на площині основи циліндра, т. е. дотичній до окружності його заснування. Звідси випливає, що точка К3 належить евольвенті окружності, так як дотичні у всіх точках циліндричної гвинтової лінії мають сліди на площині основи циліндра, що утворюють евольвенту окружності підстави цього циліндра.
Скористаємося цим для побудови дотичної до циліндричної гвинтової лінії в будь-якої її точки. На гвинтовий лінії, зображеної на рис. 306, дотична побудована в точці К. Насамперед проведена горизонтальна проекція дотичній - відрізок К'1 '- перпендикулярно до О'К'. За точці 1 'на евольвенті знайдена проекція 1 ", після чого може бути проведена фронтальна проекція дотичній - пряма 1" К ". Побудова повторено для точки L.
Можна побудувати на поверхні циліндра криву лінію, утворену так само, як і гвинтова лінія, але обертання утворює циліндра залишити рівномірним, а переміщення точки по котра утворює зробити змінним по якому-небудь закону. Такі криві іноді називають гвинтовими лініями зі змінним кроком.
Побудова дано на рис. 307 при рівномірно прискореному русі точки по котра утворює. Задані переміщення точки в кожному із зазначених дванадцяти положень утворює; наприклад, при дев'ятому положенні точка переміститься на відрізок С9 Е9 (рахуючи від восьмого положення цієї точки).
На рис. 307 дана також розгортка побудованої лінії; кут підйому змінний.
Якщо точка переміщується рівномірно по котра утворює прямого кругового конуса 1), а утворює здійснює обертальний рух навколо осі конуса з по-
1) Зображення конуса на проекційному кресленні розглядалося в курсі креслення середньої школи.
постійної кутовий швидкістю, то траєкторією точки є конічна гвинтова лінія 1); її проекції зображені на рис. 308. Переміщення точки по котра утворює пропорційні кутовим переміщенням цієї утворює. На рис. 308 зазначено
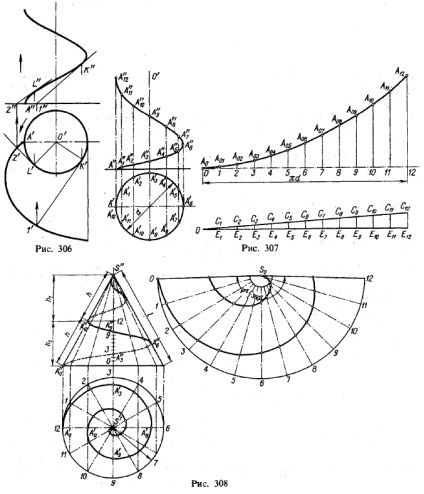
на поверхні конуса дванадцять положень утворює, і на них вказані відповідні положення точки. Відстань між точками суміжних витків A0 A12 = h, виміряний по котра утворює, називається кроком конічної гвинтової лінії 2),
1) Конічна гвинтова лінія добре ілюструється, наприклад, гвинтовий конічної пружиною або конічною різьбою.
2) Іноді крок конічної гвинтової лінії вважають за її осі. Відрізок h1 (рис. 308) є проекцією кроку h, виміряного по котра утворює, на осі гвинтової лінії. Поділу h на n рівних частин відповідає розподіл h1 на стільки ж рівних між собою частин і навпаки.
Проекція конічної гвинтової лінії на площині, паралельної осі конуса (в даному випадку фронтальна проекція), являє собою синусоїду з зменшується висотою хвилі; проекція на площині, перпендикулярній до осі конуса (в даному випадку горизонтальна проекція), являє собою спіраль Архімеда.
На розгортці бічній поверхні конуса (рис. 308, праворуч) гвинтова лінія розгорнеться також в спіраль Архімеда, так як рівномірному кутовому переміщенню радіусу на розгортці поверхні конуса відповідає рівномірний ж переміщення точки з цього радіусу. На малюнку показана розгортка для двох обертів конічної гвинтової лінії.
Гвинтова лінія може бути побудована не тільки на циліндричній або конічній поверхні. Прикладом може служити гвинтова лінія (рис. 309) на поверхні, образован-
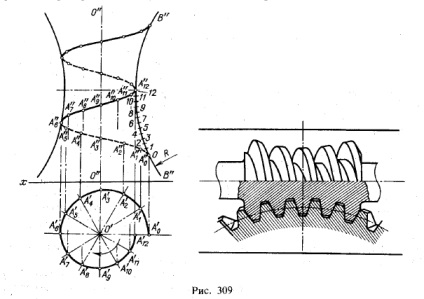
ної обертанням дуги ВВ навколо осі 00, т. е. на поверхні тора 1). Подібну кручені лінію можна бачити на глобоідальних черв'яків (див. Рис. 309, праворуч).
Питання до § 48
- Як утворюються циліндрична і конічна гвинтові лінії?
- Що називається кроком гвинтової лінії - циліндричної та конічної?
- Який вид мають проекції циліндричної і конічної гвинтових ліній на площинах - паралельної осі гвинтової лінії і перпендикулярній у цій осі?
- Як розпізнати, права чи ліва гвинтова лінія нанесена на поверхні циліндр дріческого і конічного стрижнів? Як вказати хід, якщо зображується тільки лінія?
- У що розгортається кожен виток гвинтової лінії - циліндричної та конічної?
- Як виражається крутизна підйому циліндричної гвинтової лінії?
- Яка лінія утворюється на площині, перпендикулярній до осі циліндричної гвинтової лінії, якщо побудувати сліди дотичних до цієї лінії?
1) Відомості про торі даються в курсі креслення середньої школи.