Призми виготовляють з оптичного скла і використовують для відхилення променів світла. Розглянемо хід променів світла в тригранної призмі. Якщо промінь світла падає на грань AB і виходить через грань BC, то грань BC називають підставою призми, див. Рис. Протилежний основи кут γ називають заломлюючим кутом призми. Кут Δ між напрямком променя 1 і напрямком відхиленого променя 2 називається кутом відхилення променя в призми. Кут, на який призма відхиляє (монохроматичне) промінь світла, залежить від заломлюючого кута призми γ, коефіцієнта заломлення призми n і кута падіння α 1 (див. Рис.)
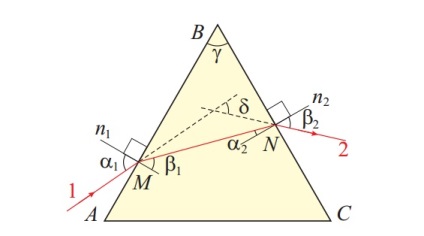
Мал. Луч 1 падає на грань AB тригранної призми, заломлюється, падає на грань BC. переломлюється і виходить (промінь 2) з призми. При проходженні через призму промінь світла відхиляється на кут Δ. який залежить від оптичної щільності матеріалу призми n і від заломлюючого кута призми Показані нормалі n1 і n2 до заломлюючим гранях призми. Видно, що промінь світла, що пройшов через призму, відхиляється до основи AC. При ламанні в точці M кути падіння α1 і заломлення β1 пов'язані рівністю
З трикутника MNB знаходимо кут падіння α 2 променя на грань призми BC. Кут доповнює кут β1 до прямого кута, тому
Аналогічно, кут доповнює кут α 2 до прямого кута, тому
Оскільки сума кутів в трикутнику дорівнює Π. отримуємо
Кути α 2 і β 2 пов'язані співвідношенням
У точці M промінь відхиляється на кут α 1 і β1. а в точці N - на кут β 2 - α 2. Тому повний кут відхилення променя Δ призмою дорівнює сумі відхилень в точках M і N
Підставляючи сюди значення α 2 з (2), отримуємо
Використовуючи рівності (1) - (4) і знаючи n і γ. можна обчислити кут Δ відхилення променя призмою для кожного кута падіння α 1.