Ії того, що дві прямі схрещуються

прямі l1 і l2 називаються перехресними, якщо вони не лежать в одній площині. Нехай а і b - напрямні вектори цих прямих, а точки M1 і M2 належать відповідно прямим і l1 і l2

Ії того, що дві прямі схрещуються
Тоді вектори а, b, M1M2 »не компланарність, і тому їх змішане твір не дорівнює нулю, т. Е. (А, b, M1M2>) = / = 0.Верно і зворотне твердження: якщо (а, b, M1M2> ) = / = 0, то вектори а, b, M1M2 »не компланарність, і, отже, прямі l1 і l2 чи не лежать в одній площині, т. е. скрещіваются.Такім чином, дві прямі схрещуються тоді і тільки тоді, коли виконано умова (а, b, M1M2>) = / = 0, де а і b - напрямні вектори прямих, а M1 і M2 - точки, що належать відповідно до даних прямим. Умова (а, b, M1M2>) = 0 є необхідною і достатньою умовою того, що прямі лежать в одній площині. Якщо прямі задані своїми канонічними рівняннями

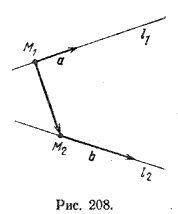
то а = (а1; а2; а3), b = (b1; b2; b3), М1 (x1; у1; z1), М2 (х2; у2; z2) і умова (2) записується таким чином:

Відстань між перехресними прямими

це відстань між однією з перехресних прямих і паралельної їй площиною, що проходить через іншу прямую.Расстояніе між перехресними прямими - це відстань від деякої точки одній з перехресних прямих до площини, що проходить через іншу пряму паралельно першої прямої.

26.Определеніе еліпса, канонічне рівняння. Висновок канонічного рівняння. Властивості.

Еліпсом називається геометричне місце точок площини, для яких сума відстаней до двох сфокусованих точок F1 і F2 цієї площини, які називаються фокусами є величина постоянная.Прі цьому не виключається збіг фокусів елліпсіса.Еслі вокуси збігаються то еліпсис є окружность.Для будь-якого еліпса можна знайти декартову систему координат таку, що еліпс буде описуватися рівнянням (канонічне рівняння еліпса):

Воно описує еліпс з центром на початку координат, осі якого збігаються з осями координат.

Якщо ж в правій частині стоїть одиниця зі знаком мінус, то вийшло рівняння:

описує уявний еліпс. Зобразити такий еліпс в дійсній площині невозможно.Обозначім фокуси через F1 і F2, а відстань між ними через 2с, а суму відстаней від вироб-вільної точки еліпса до фокусів - через 2а

Для виведення рівняння еліпса виберемо систему координат Оху так, щоб фокуси F1 і F2 лежали на осі Ох, а початок координат збігалося з серединою відрізка F1F2. Тоді фокуси матимуть такі координати: іПусть М (х; у) - довільна точка еліпса. Тоді, згідно з визна-поділу еліпса. т. е.

Це, по суті, і є рівняння еліпса.

27.Визначення гіперболи, канонічне рівняння. Висновок канонічного рівняння. властивості

Гіперболою називається геометричне місце точок площини, для якої абсолютна величина різниці відстані до двох фіксованих точок F1 і F2 цієї площини, які називаються фокусами, є величина постоянная.Пусть M (x; y) - довільна точка гіперболи. Тоді згідно з визначенням гіперболи | MF1 - MF2 | = 2a або MF1 - MF2 = ± 2a,

Ії того, що дві прямі схрещуються

28.Определеніе параболи, канонічне рівняння. Висновок канонічного рівняння. Властивості. Параболою називається ГМТ площині, для яких відстань до деякої фіксованої точки F цій площині дорівнює відстані до деякої фіксованої прямої, також розташованої в даній площині. F - фокус параболи; фіксована пряма - директриса параболи. r = d,

r =; d = x + p / 2; (X-p / 2) 2 + y 2 = (x + p / 2) 2; x 2 -xp + p 2/4 + y 2 = x 2 + px + p 2/4; y2 = 2px;

Властивості. 1.Парабола має вісь симетрії (вісь параболи); 2.Вся

парабола розташована в правій півплощині площині Oxy при p> 0, і в лівій

якщо p<0. 3.Директриса параболы, определяемая каноническим уравнением, имеет уравнение x= -p/2.

Схожі статті