Деякі S не є P.
постане в наступному вигляді:
├.
Подібним же чином ми можемо записати інші силогізми: як безпосередні, так і опосередковані.
§ 4. Способи перевірки правильності силогізмів
Завдання логіки - відокремлювати правильні міркування від неправільнщх. Природно, цю ж задачу доводиться вирішувати і по відношенню до силлогизмам. Практично всі міркування, наведені раніше (за винятком прикладу міркування в діалозі з § 1 цієї глави), є правильними. Але ми знаємо з практики нашого щоденного спілкування, що взагалі-то неправильні міркування зустрічаються досить часто. Виникає запитання: яким чином критикувати неправильні міркування? Цю задачу вирішують способи перевірки правильності силогізмів.
Всього таких способів три:
1) побудова кругових схем для посилок і укладання силогізмів;
2) пред'явлення контрпримера;
3) перевірка на відповідність загальним правилам силогізмів і правилам фігур.
Розглянемо ці способи окремо.
1) Побудова кругових схем для посилок і поєднання їх на одній схемі.
Це - найпростіший спосіб перевірки. У правильному силогізм суміщення кругових схем, побудованих для кожної з посилок, має дати однозначну результат, що співпадає зі ставленням між меншим і більшим терміном в ув'язненні.
Всі юристи знають ознаки злочину.
Ніхто з присутніх не знає ознак злочину.
Ніхто з присутніх не є юристом.
Це - друга фігура, модус АЕЕ.
Позначимо терміни: "юрист" - черезP. "Людина, яка знає ознаки злочину" - черезM. "Присутній" -черезS. Тоді для більшої посилки ми отримаємо наступну схему:
Для другої посилки, відповідно, наступну схему:
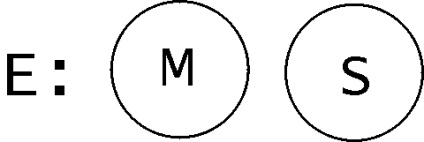
Поєднання цих схем дасть наступний результат:
Ми бачимо, що інших відносин між S і P бути не може. тобто ми получіліоднозначний результат. Наш висновок «Ні одінSне естьP» на цій схемі істинно. Це означає, що при істинності посилок висновок обов'язково істинно, а значить вихідне умовивід правильно.
Всі юристи знають ознаки злочину.
Всі присутні знають ознаки злочину.
Всі присутні є юристами.
Це також друга фігура, модус ААА. Позначимо терміни силогізму так само, як в попередньому прикладі. Тоді для більшої посилки вийде схема, як в предшествсющем прикладі.
Для меншою посилки вийде наступна схема:
Поєднуємо ці схеми на одній коловою схемою:
Ми бачимо, що ці схеми можна поєднати по-різному. тобто ми не отримали однозначного результату. Причому на суміщеної схемою (а) наш висновок істинно, а на суміщеної схемою (б) наше висновок хибний. Як інтерпретувати результати нашого поєднання кругових схем для посилок? Згадаймо, що в правильному дедуктивний умовивід посилки і висновок повинні знаходитися у відношенні логічного слідування. Разом з тим ми знаємо, що відношення логічного слідування відсутній там, де посилки можуть бути істинними, а висновок помилковим. (Згадайте наші відносини між складними судженнями!) Ці відносини ми можемо перенести і на суміщені кругові схеми і сказати, що якщо існує така поєднана схема, на якій посилки істинні, а висновок хибний, то наш силогізм не є правильним. У нашому випадку така схема існує - це схема (б). Отже, наш силогізм неправильний.
Звідси ммжно отримати загальний критерій правильності силогізмів:
Силогізм являетсяправільним, еслінельзя построітьтакую поєднану кругову схему, на якій обидві посилки є істинними, а висновок - хибним.
Звідси випливає і критерій неправильності силогізмів:
Силогізм являетсянеправільним, есліможно построітьхотя б одну таку кругову схему, на якій обидві посилки є істинними, а висновок - хибним.
Приклад. Застосуємо розроблений метод для обговорення міркування про спартанців і їх внесок в філософію, який поставив в глухий кут персонажів нашого діалогу в § 1 цієї глави. Відтворимо останній з обговорюваних там силогізмів ще раз.
Деякі стародавні греки внесли вклад в розвиток філософії.
Всі спартанці - стародавні греки.
Деякі спартанці внесли вклад в розвиток філософії.
Це - перша фігура, модус IAI. Позначимо більший термін - "ті, хто зробив внесок в розвиток філософії" - черезP. середній - "стародавні греки" - черезM. а менший - "спартанці" - черезS. Тоді кругова схема, відповідна більшою посилці, буде виглядати наступним чином:
а кругова схема, відповідна меншою посилці:
Cовместів їх, отримуємо:
На цій діаграмі висновок "Деякі спартанці внесли вклад в розвиток філософії" - помилково а обидві посилки істинні. Отже, може бути побудована така поєднана схема, на якій посилки істинні, а висновок - помилково, а значить, що розглядається умовивід неправильно.
Пояснення. Побудова кругових схем - це не аргумент в суперечці. Навряд чи вам кого-небудь вдасться переконати в своїй правоті, якщо ви будете малювати схеми. Однак вони допоможуть усвідомити вам ситуацію, зрозуміти, що ж неправильно в аргументації Вашого опонента, і задати йому, наприклад, таке питання: "Ви впевнені, що спартанці відносяться саме до тих грекам, які внесли вклад в філософію? А чи не може бути так, що вони належать саме до тієї частини греків, які ніякого вкладу в філософію не вносили? "І нехай тепер він спробує більш-менш переконливо відповісти на ваші запитання. Ініціатива перейшла до вас. А сформулювати такі питання, які представляють складне становище для опонента, допомогли нам саме кругові схеми, які наочно показують, що саме потрібно запитати.
2) Пред'явлення контрпримера.
Спосіб виявлення неправильності умовиводів шляхом побудови кругових схем все ж не приводить до переконливої перемоги в дискусії. Він, скоріше, носить теоретичний характер. Як же спростовувати висновки на практиці так, щоб неправильність умовиводу Вашого опонента була б всім абсолютно очевидною і тим самим забезпечувала б вам перемогу в суперечці? Для цієї мети підходить пред'явленіеконтрпрімера.
Контрпрімер- силогізм, тотожний з даними за формою (тобто має ту ж фігуру і той же модус), але абсурдний за змістом.
Що значить «абсурдний за змістом»? Це означає, що посилки контрпримера повинні бути очевидно істинними судженнями, а заключеніеочевідно хибним. Це і справляє враження абсурдності умовиводи. Підставою методу контрпримера є живе в нашій душі вимога до правильних висновків: в них з істинності посилок обов'язково повинна слідувати істинність висновку, а якщо висновок (при істинних посилках) явно помилково, то це наше почуття обурюється і свідчить проти даного умовиводи.
По відношенню до висновку про спартанців і філософії завдання пошуку і пред'явлення контрпримера вирішується таким чином. Ми шукаємо умовивід по першій фігурі, модус IАI. Цей модус, як ми тепер знаємо, не відноситься до числа правильних. Однак нам це ще треба продемонструвати аудиторії. Як показує побудована раніше кругова схема, нам потрібно знайти такі понятіяM іP. які перебували б у відношенні перехрещення, і таке понятіеS. обсяг якого очевидно виключався б з обсягу понятіяP. Тут потрібен якийсь творчість. Але, принаймні, кругові схеми показують, що шукати. Візьмемо в якості термінів нашого контрпримера "люди", "ті, хто можуть народжувати дітей", і "чоловіки", відповідно. Тоді у нас вийде наступне умовивід:
Деякі люди можуть рмжать дітей.
Деякі чоловіки можуть народжувати дітей.
Цей висновок є контрприклад. тому що воно має в точності ту ж форму, що і умовивід про спартанців і філософії, його посилки очевидно істинні, а висновок ще більш очевидно помилково. Мало того, якщо б така ситуація зустрілася в реальному дискусії, цей контрприклад справив би до того ж ще і комічний ефект, і Ваш опонент був би убитий остаточно.
Для силогізму, говорить про юристів і ознаках престунленія, можна побудувати наступний (більш серйозний) контрприклад:
Всі дурні люди повинні підкорятися закону.
Всі розумні люди повинні підкорятися закону.
Всі розумні люди дурні.
Побудувавши контрприклад, нам слід звернутися до нашого опонента з приблизно такою промовою: "Ваше міркування нікуди не годиться, тому що, слідуючи Вашій логіці, можна побудувати таке міркування" і потім приводите Ваш контрприклад.
3) Перевірка на відповідність загальним правилам силогізму і правилам фігур.
Для вирішення завдання відділення правильних силогізмів від неправильних в логіці були сформульовані спеціальні правила. Порушення хоча б одного з цих правил призводить до неправильності силогізму, дотримання всіх правил говорить про те, що силогізм правильний.
Правила силогізмів діляться на правила термінів та правила фігур.
ПТ1. У всякому силогізм має бути рівно три терміни.
Приклад. Розглянемо силогізм:
Всякий пошук істини заслуговує на повагу.
Будь-яка наука є пошук істини.
Будь-яка наука заслуговує на повагу.
МЩ бачимо, що тут рівно три терміни: "пошук істини", "те, що заслуговує на повагу", "наука". Тому вийшов силогізм.
Усі промовці пихаті.
Цицерон був консулом Риму.
З цих посилок не можна зробити ніякого висновку, тому що тут чотири терміна, а отже, немає середнього терміна, який би пов'язував посилки і дозволяв вивести висновок. Хоча, звичайно, про себе ми і здогадуємося про те, що Цицерон був оратором, але з чистою совістю не можемо зробити ніякого висновку, поки це не буде висловлено явно.
Іноді в силогізм буває чотири терміна, хоча на перший погляд здається, що їх тільки три. Це може бути пов'язано, наприклад, з омонімією.
Лук є зброя дикунів.
Ця рослина є цибуля.
Ця рослина є зброя дикунів.
Очевидно, що тут під одним словом "лук" ховаються два поняття.
З порушенням цього правила пов'язана помилка "учетверение термінів". Приклади цієї помилки ми тільки що проаналізували.
ПТ2. Середній термін повинен бути розподілений хоча би в одній з посилок.
Нрімер. Розглянемо умовивід про науку з ПТ1. У ньому середній термін "пошук істини" розподілений в більшій посилці.
Всі твори класичної літератури захоплюючі.
Деякі детективи захоплюючі.
Деякі детективи є творами класичної літератури.
Ув'язнення не випливає з посилок, тому що середній термін «захоплююче твір» не розподілений ні в одній з посилок, хоча і вірно, що деякі детективи є творами класичної літератури. Досить вспммніть, наприклад, "Злочин і кара" Федора Достоєвського. Однак це не робить наведене умовивід правильним.
ПТ3. Термін, розподілений в ув'язненні, повинен бути розподілений в посилці.
Приклад. У силогізм з ПТ1 термін "наука" розподілений в ув'язненні, але він розподілений і в меншій посилці.
Всі справжні філософи неупереджені.
Жоден політик не є справжнім філософом.
Жоден політик не є неупередженим.
У цьому прикладі термін "неупереджена людина" розподілений в ув'язненні і не розподілений в посилці. І хоча висновок тут, швидше за все, істинно, все умовивід є неправильним.
ПП2. З двох негативних суджень не можна вивести ніякого висновку.
Приклад. З посилок:
Жоден юрист не є неупередженим.
Жоден історик не є неупередженим.
Нічого не можна вивести про сомтношеніі термінів "історик" і "юрист".
ПП3. Висновок негативно, якщо і тільки якщо одна з посилок негативна.
Це правило очевидно.
ПП4. З двох приватних суджень не можна вивести ніякого висновку.
Приклад. З міркувань:
Деякі художники заслуговують захоплення.
Деякі модерністи - художники.
Не можна вивести ніякого висновку.
ПП5. Якщо одна з посилок - приватне судження, то і висновок повинен бути приватним.
Це правило також очевидно.
За допомогою цих восьми правил ми можемо з 256 модусів силогізму відібрати правильні.
Однак в логіці були вироблені також і правила для фігур, щоб можна було в разі кожної окремої фігури дати критерії правильності умовиводів, пристосовані саме для цієї фігури.
В силу того, що IV фігура рідко застосовується в практиці міркувань, а правила для неї досить складні, ми не будемо їх розглядати.
I фігура .У умовиводах по першій фігурі менша посилка повинна бути ствердною, а велика - загальної.
Приклад. Силогізм по першій фігурі:
Всі студенти - люди.
Жоден професор не є студентом.
Жоден професор не є людиною.
є неправильним, тому що менша посилка в ньому негативна.
Деякі люди заслуговують на повагу.
Всі злочинці - люди.
Деякі злочинці заслуговують на повагу.
Цей силогізм по першій фігурі неправильний, тому що велика посилка є приватним судженням.
II фігура .Одна з посилок повинна бути негативною, а велика - загальної.
Все фізики прагнуть до істини.
Деякі історики прагнуть до істини.
Деякі історики є фізиками.
Цей висновок по другій фігурі неправильно, тому що обидві посилки - позитивні судження.
Приклад. Силогізм по другій фігурі:
Деякі люди можуть бути батьками.
Жодна жінка не може бути батьком.
Деякі жінки не можуть бути людьми.
неправильний, тому що велика посилка - приватне судження.
III фігура .Меньшая посилка повинна бути ствердною, а висновок - приватним.
Всі студенти є людьми.
Деякі студенти не є чоловіками.
Деякі чоловіки не є людьми.
Цей силогізм по третій фігурі не є правильним, тому що менша посилка в ньому негативна.
Всі студенти є людьми.
Всі студенти є живими істотами.
Всі живі істоти є студентами.
Цей силогізм по третій фігурі неправильний, тому що укладенням його є загальне судження.
Керуючись загальними правилами силогізму і правилами фігур, легко можна відрізняти правильні модуси силогізмів від неправильних. Звичайно, пред'явлення контрпримера більш приваблива процедура. Однак в ній бракує систематичності і обгрунтованості. Правила дозволяють систематично відкидати неправильні умовиводи і обґрунтовувати прийнятність правильних висновків. Якщо ми встановлюємо, що силогізм виконує всі правила, то ми можемо бути впевнені, що він - правильний. Вправа в застосуванні цих правил до конкретних силлогизмам поступово допоможе вам розвинути навички отличения правильних висновків від непрааільних. Це і є логічна культура.