Простим вирахуванням легко переконатися в справедливості рівності
Додавши до обох частин цієї рівності число, отримаємо нове рівність
в якому, як неважко помітити, права і ліва частини являють собою повні квадрати, т. е.
Отримуючи з правої і лівої частин попереднього рівності квадратний корінь, одержуємо рівність:
звідки випливає, що
За визначенням являє собою деякий невід'ємне число, яке, будучи зведено в квадрат, дастх. Ясно, що з цим визначенням задовольняють два числа, а саме х і х. Отже, якщо число х неотрицательно (х> 0), то = х; якщо ж число х негативно, тобто число х позитивно, то = - x. Звідси робимо висновок, що (властивість арифметичного квадратного кореня), що не враховується в змісті цих софізмів і призводить до помилкових висновків.
«Будь-яке число дорівнює своїй половині.»
Запишемо очевидне для будь-якого числа a тождествоa2- a2 = a2- a2, де а-будь-яке число.
Винесемо a в лівій частині за дужку, а праву частину розкладемо на множники за формулою різниці квадратів, отримаємо a (a - a) = (a + a) (a - a).
Розділивши обидві частини на a - a. отримаємо a = a + a. або a = 2a.
Розділимо на 2 і отримаємо а = а / 2
Ми ділимо обидві частини на нуль, а розподіл на нуль заборонено.
«Через точку на пряму можна опустити два перпендикуляра»
Спробуємо "довести", що через точку, що лежить поза прямою, до цієї прямої можна провести два перпендикуляра. З цією метою візьмемо трикутник АВС. На сторонах АВ і ВС цього трикутника, як на діаметрах, побудуємо півкола. Нехай ці півкола перетинаються зі стороною АС в точках Е і D. З'єднаємо точки Е і D прямими з точкою В. Кут АЕВ прямий, як вписаний, що спирається на діаметр; кут ВДС також прямий. Отже, ВЕ перпендикулярна АС і ВD перпендикулярна АС. Через точку В проходять два перпендикуляра до прямої АС.
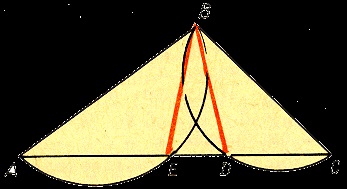
Міркування, про те, що з точки на прямій можна опустити два перпендикуляра, спиралися на хибний креслення. Насправді півкола перетинаються зі стороною АС в одній точці, тобто ВЕ збігається з ВD. Значить, з однієї точки на прямій можна опустити два перпендикуляра.
Будь-яке позитивне число є негативним.
Нехай n-позитивне число.
Візьмемо інше довільне позитивне число a і помножимо обидві частини нерівності на (-а): -2an + a<-2an.
Віднімаючи з обох частин цієї нерівності величину (-2an), отримаємо нерівність a<0, доказывающее, что всякое положительное число является отрицательным.
При множенні на негативне число знак нерівності змінюється.