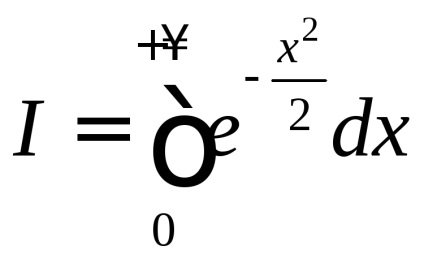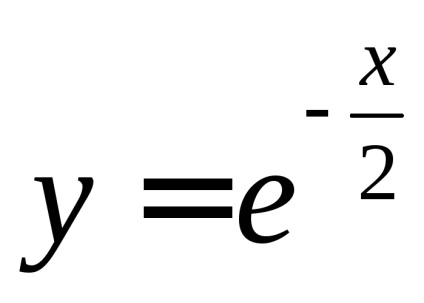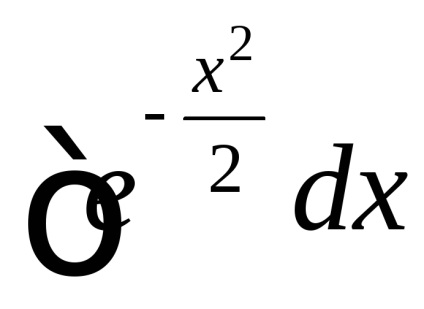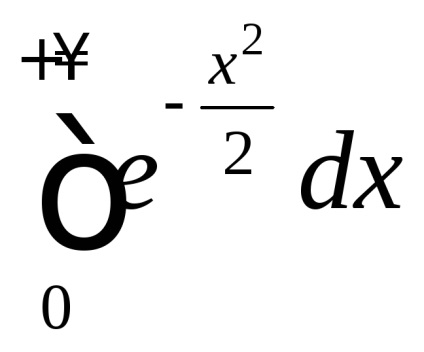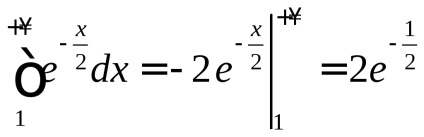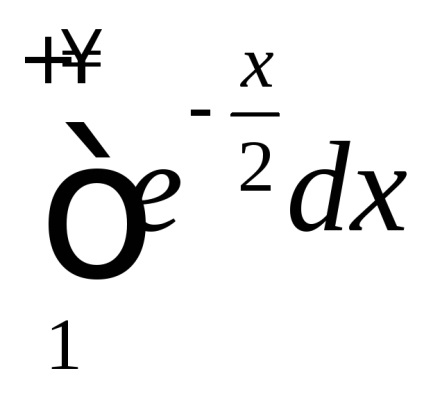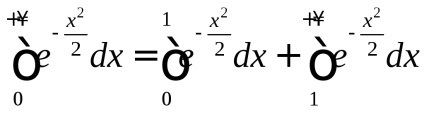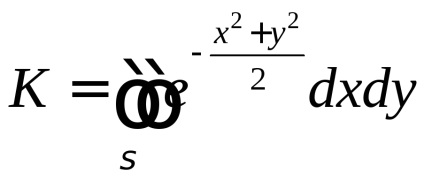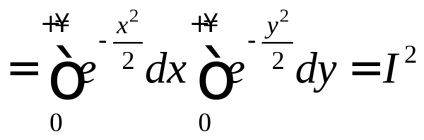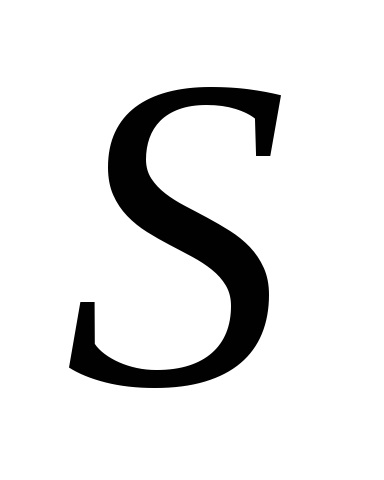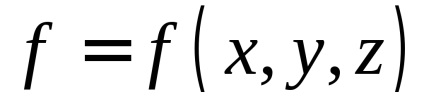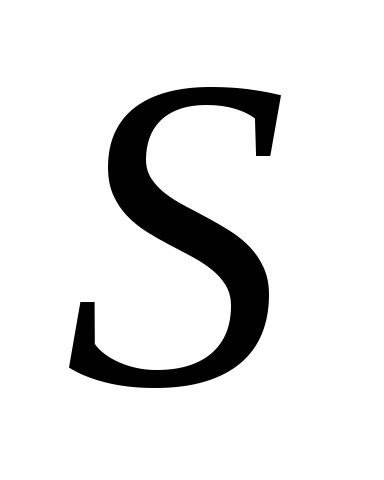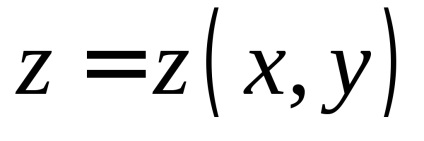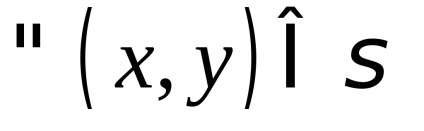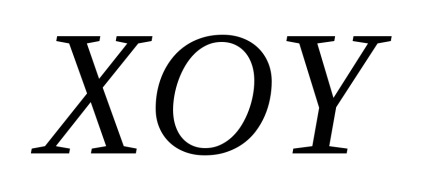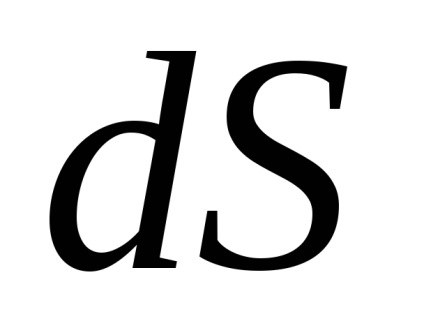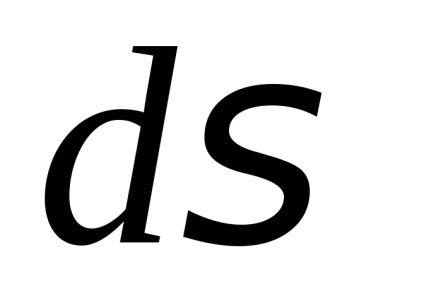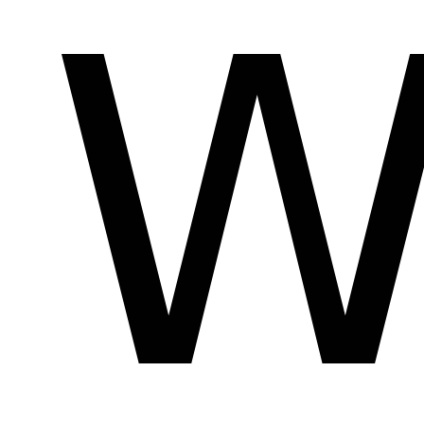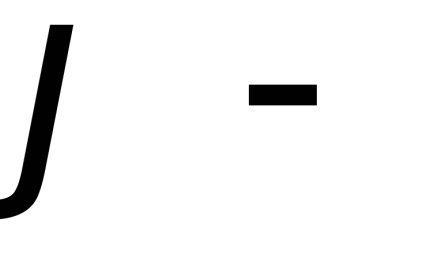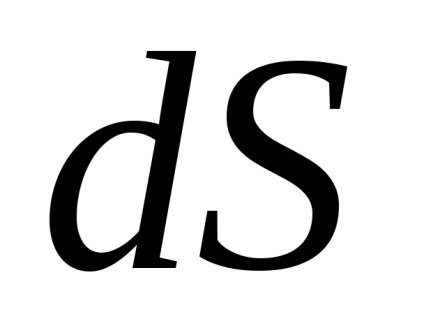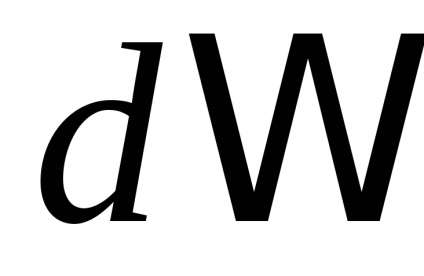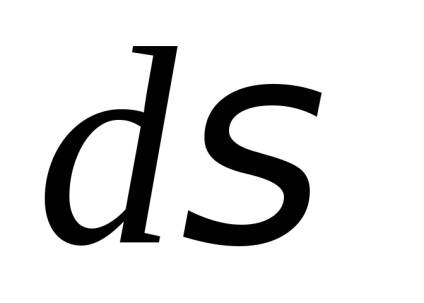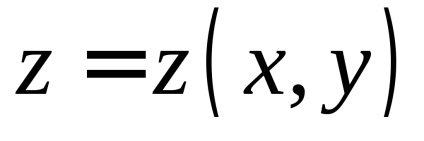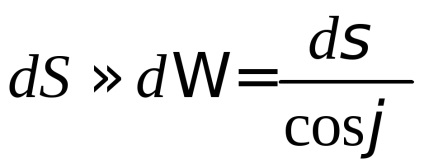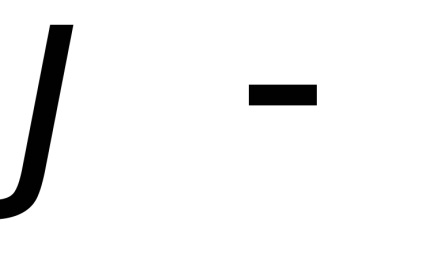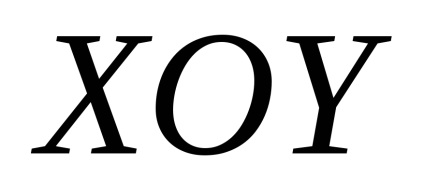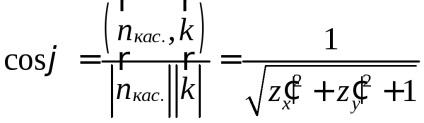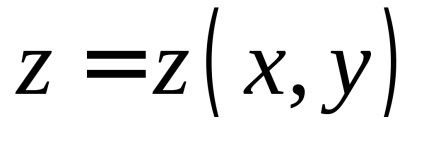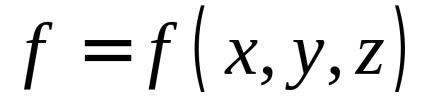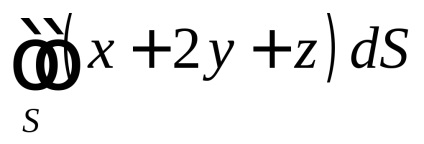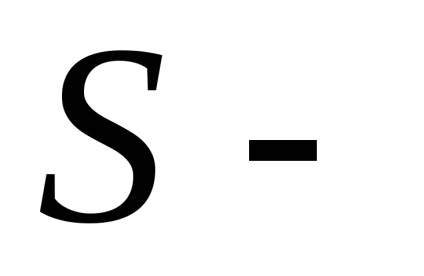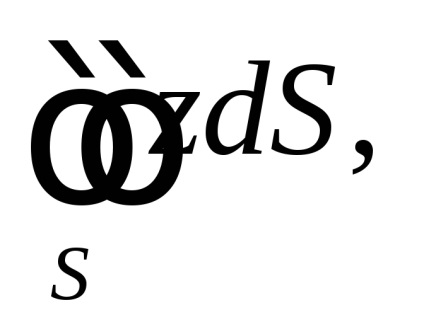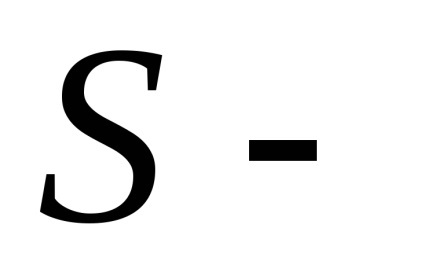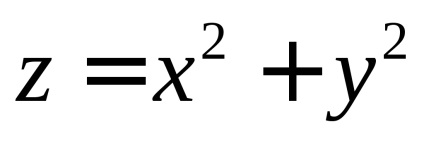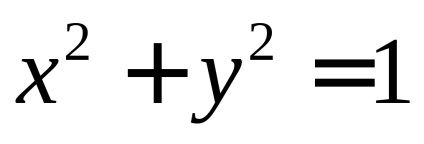У теорії ймовірностей велику роль відіграє невласний інтеграл
, який називається інтегралом Пуассона. Як було відзначено в розділі 7, функція
не має елементарної первісної, і невизначений інтеграл
відноситься до так званих «неберущімся» интегралам. Однак, обчислити невласний
можна, можливо. Перш, ніж знайти його значення, переконаємося в тому, що він сходиться.
Так як, то, але
, тобто за визначенням збіжності невласних інтеграловI роду
сходиться. Тому
сходиться за ознакою порівняння.
Для обчислення значення інтеграла Пуассона застосуємо такий штучний прийом: розглянемо подвійний інтеграл
, де областю інтегрування є перша чверть координатної площини (ріс.56).
В декартових координатах
(Згадаємо, що величина певного інтеграла не залежить від позначення змінної інтегрування).
З іншого боку, переходячи до полярної системі координат, отримаємо:
.
8.13. Обчислення поверхневого інтеграла першого роду (по площі поверхні)
Нехай на поверхні
, задається рівнянням, визначена неперервна функція
. За визначенням поверхневим інтегралом першого роду від цієї функції називається
,
де точки, а
- малі частини поверхні
, на які вона розбивається при складанні інтегральної суми (рис.10).
Будемо вважати, що функція
дифференцируема
, тобто в будь-який точкеS можна провести дотичну площину.
область
є проекцією
на площину
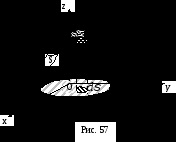
. Висловимо елемент поверхні
через його проекцію
(Ріс.57). Для цього скористаємося відомим твердженням: якщо
- проекція плоскою області з площею
, то
, де
кут між площиною області і площиною проекції.
Проведемо в довільній точці обраного елемента поверхні
дотичну площину і нехай
- та її частина, яка проектується на
. Так як функція
дифференцируема, то площа елемента
, де
кут між дотичній площиною і площиною
, який дорівнює куту між їх нормалями.
обчислимо
. Якщо переписати рівняння поверхні
в неявному вигляді, то (див. гл. 6), апоетому
(Див. Гл. 2).
У точках поверхні
, де
, функція
приймає значення, тому відповідно до визначення поверхневий інтеграл першого роду може бути зведений до подвійного інтеграла:
Таким чином, обчислення поверхневого інтеграла першого роду зводиться до обчислення подвійного інтеграла по проекції даної поверхні на площину
.
ЗАУВАЖЕННЯ. якщо поверхня
зручно проектувати на іншу координатну площину, то формули (8.17) і (8.18) відповідним чином зміняться.
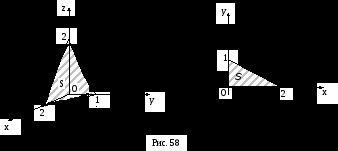
П
РИМЕР. обчислити
, якщо
частина площині, розташована в першому Октант (ріс.58).
З рівняння площини отримаємо:
. Крім того, у всіх точках площини, Тому-за властивістю 1 визначеного інтеграла: площа проекції
(Ріс.58), очевидно, дорівнює 1.
Розглянемо трохи складніший приклад.
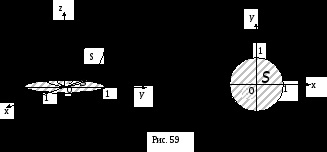
ПРИКЛАД. обчислити
якщо
частина поверхні еліптичного параболоїда
, вирізати з нього циліндром
(Ріс.59).
Схожі статті